Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Δίνεται τρίγωνο ΑΒΓ με ΑΔ και ΑΕ αντίστοιχα η εσωτερική και η εξωτερική
διχοτόμος της γωνίας
Α
(Δ, Ε σημεία της ευθείας ΒΓ). Φέρουμε ΒΖ κάθετη στην
ΑΔ και ΒΗ κάθετη στην ΑΕ και θεωρούμε Μ το μέσο του ΒΓ. Να αποδείξετε ότι:
α) το τετράπλευρο ΑΖΒΗ είναι ορθογώνιο
(Μονάδες 5)
β) η γωνία
ΗΖΑ
είναι ίση με τη γωνία
ΖΑΓ
(Μονάδες 6)
γ) η ευθεία ΗΖ διέρχεται από το Μ
(Μονάδες 6)
δ)
+
=
ΑΒ ΑΓ
ΜΗ
2
.
(Μονάδες 8)
Απάντηση:
α) Είναι
+
= + = + =
= =
0
εξ
εξ
0
A
A A
A
180
HAZ HAΒ ΒAΔ
90
2 2 2
2
.
Επομένως, οι ΑΔ και ΑΕ τέμνονται κάθετα, δηλαδή
⊥
ΗΑ ΑΖ
. Άρα, το
τετράπλευρο ΑΖΒΗ έχει τρεις γωνίες ορθές οπότε θα έχει ορθή και την τέταρτη
άρα, έχει όλες του τις γωνίες ίσες και ορθές άρα, είναι ορθογώνιο
παραλληλόγραμμο.
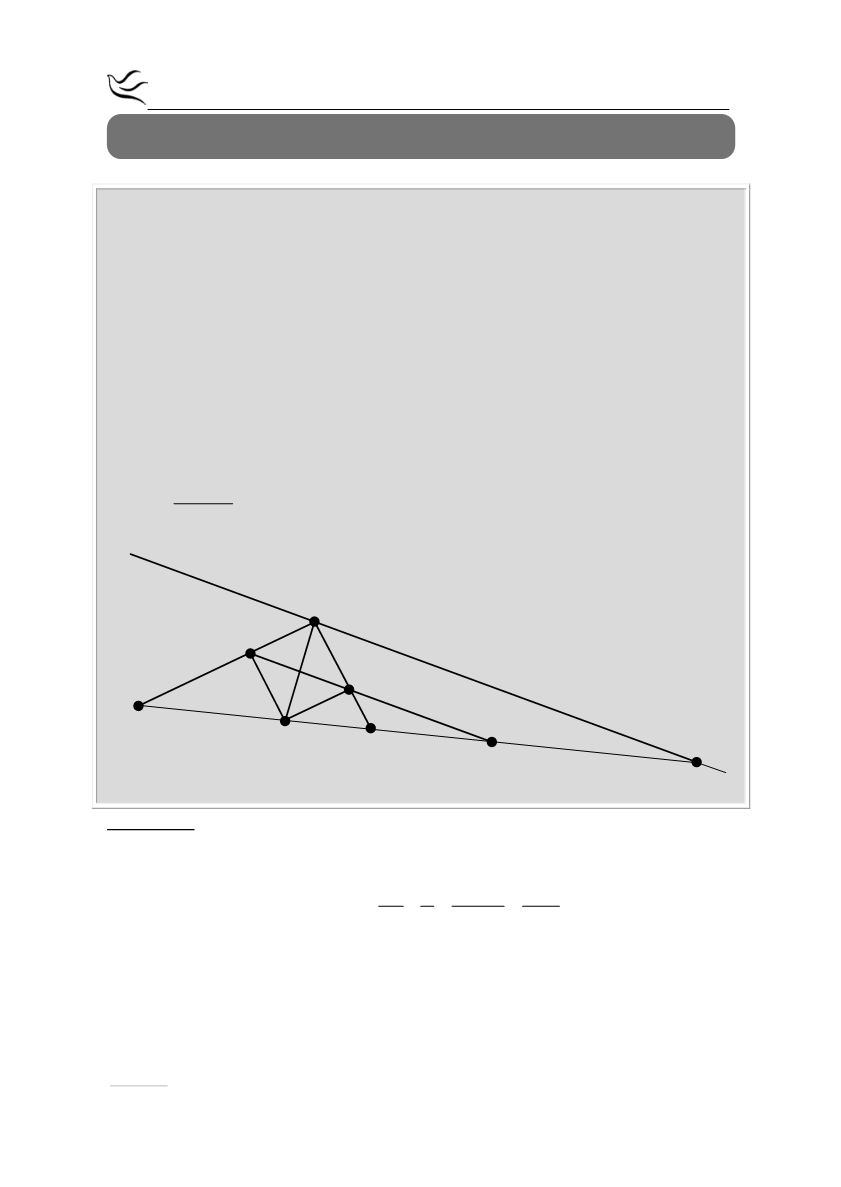
Μ
Ζ
Β
Ε
Η
Δ
Α
Γ
ΘΕΜΑ 4579
164









