Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
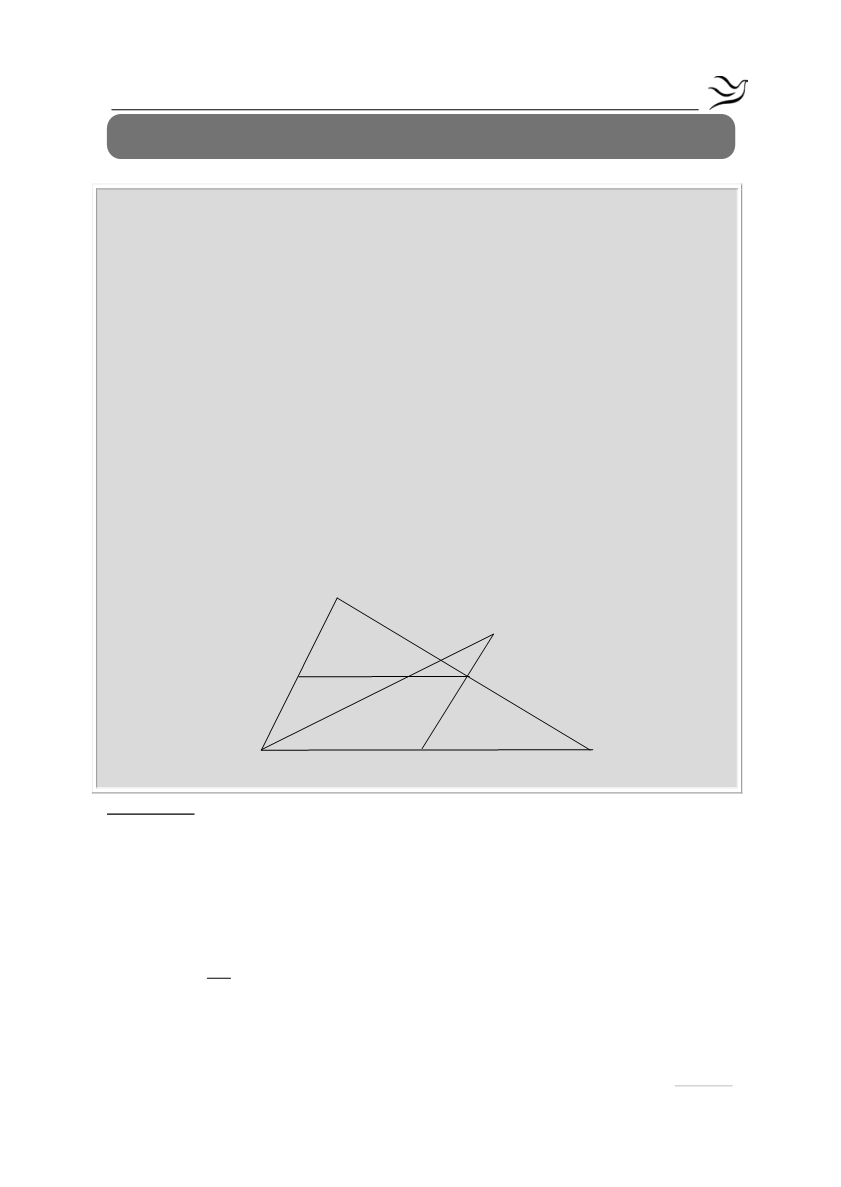
Δίνεται τρίγωνο ΑΒΓ με ΑΓ > ΑΒ και Δ, Ε, Ζ τα μέσα των πλευρών του ΒΓ, ΑΓ, ΑΒ
αντίστοιχα. Αν η διχοτόμος της γωνίας
Β
τέμνει την ΖΕ στο σημείο Μ και την
προέκταση της ΔΕ στο σημείο Ν, να αποδείξετε ότι:
α) το τετράπλευρο ΖΕΔΒ είναι παραλληλόγραμμο
(Μονάδες 7)
β) τα τρίγωνα ΒΖΜ και ΜΕΝ είναι ισοσκελή
(Μονάδες 10)
γ) ΒΖ + ΝΕ = ΔΓ.
(Μονάδες 8)
Απάντηση:
α) Στο τρίγωνο ΑΒΓ είναι
•
Ε μέσο της ΑΓ
•
Δ μέσο της ΒΓ.
Άρα,
=
ΑΒ
ΔΕ //
2
οπότε
ΔΕ//ΒΖ (1).
Δ
Ε
Β
Α
Γ
Μ
Ζ
Ν
ΘΕΜΑ 3932
159









