Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
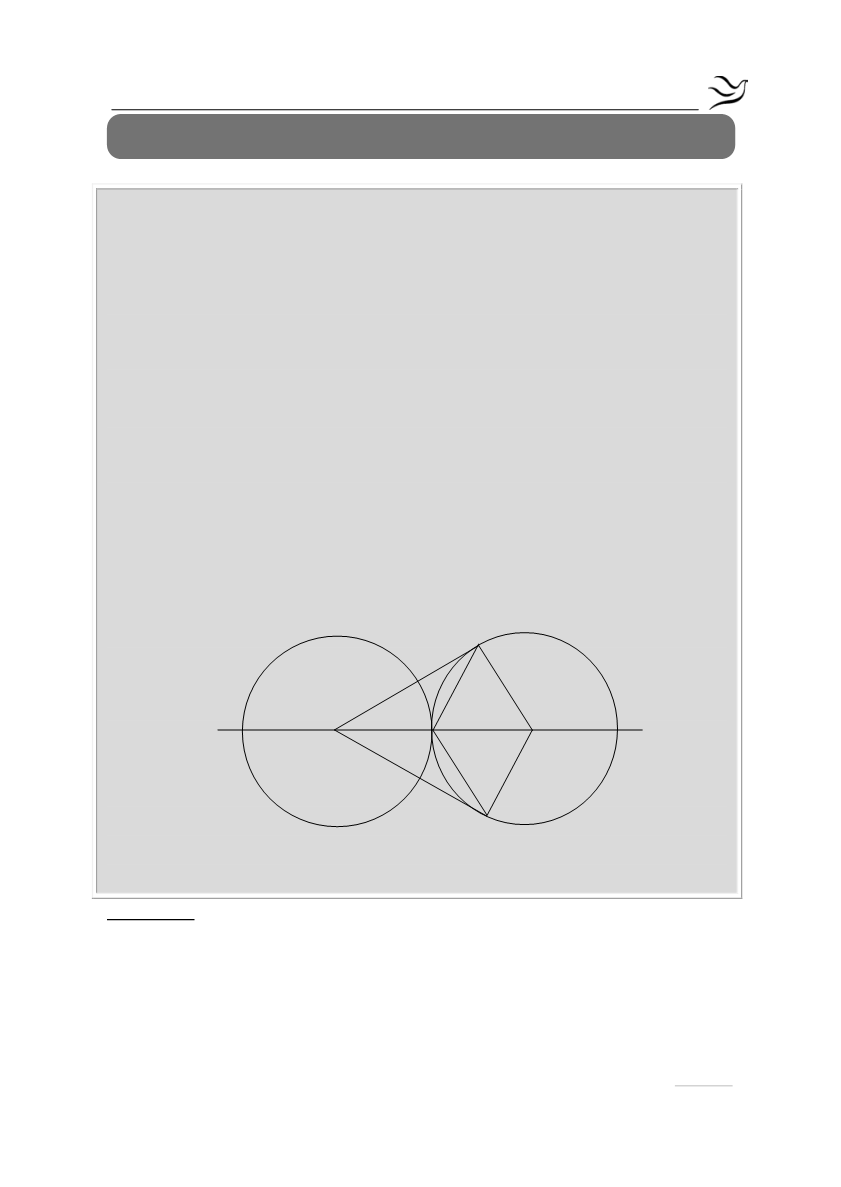
Δυο ίσοι κύκλοι (Ο, ρ) και (Κ, ρ) εφάπτονται εξωτερικά στο σημείο Ε. Αν ΟΑ
και ΟΒ είναι τα εφαπτόμενα τμήματα από το σημείο Ο στον κύκλο (Κ, ρ) να
αποδείξετε ότι:
α) ΑΕ=ΒΕ
(Μονάδες 9)
β)
=
0
ΑΟΚ 30
(Μονάδες 8)
γ) το τετράπλευρο ΑΚΒΕ είναι ρόμβος.
(Μονάδες 8)
Απάντηση:
α) Επειδή ΟΑ και ΟΒ είναι τα εφαπτόμενα τμήματα από το σημείο Ο στον κύκλο
(Κ, ρ) είναι
⊥
ΟΑ ΑΚ
και
⊥
ΟΒ ΒΚ
.
Άρα, τα τρίγωνα ΟΑΚ και ΟΒΚ είναι ορθογώνια με
= =
0
ΟΑΚ ΟΒΚ 90
.
Ακόμη, επειδή οι κύκλοι είναι ίσοι θα είναι
ΘΕΜΑ 3908
Α
Β
Ε
Κ
Ο
155









