Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
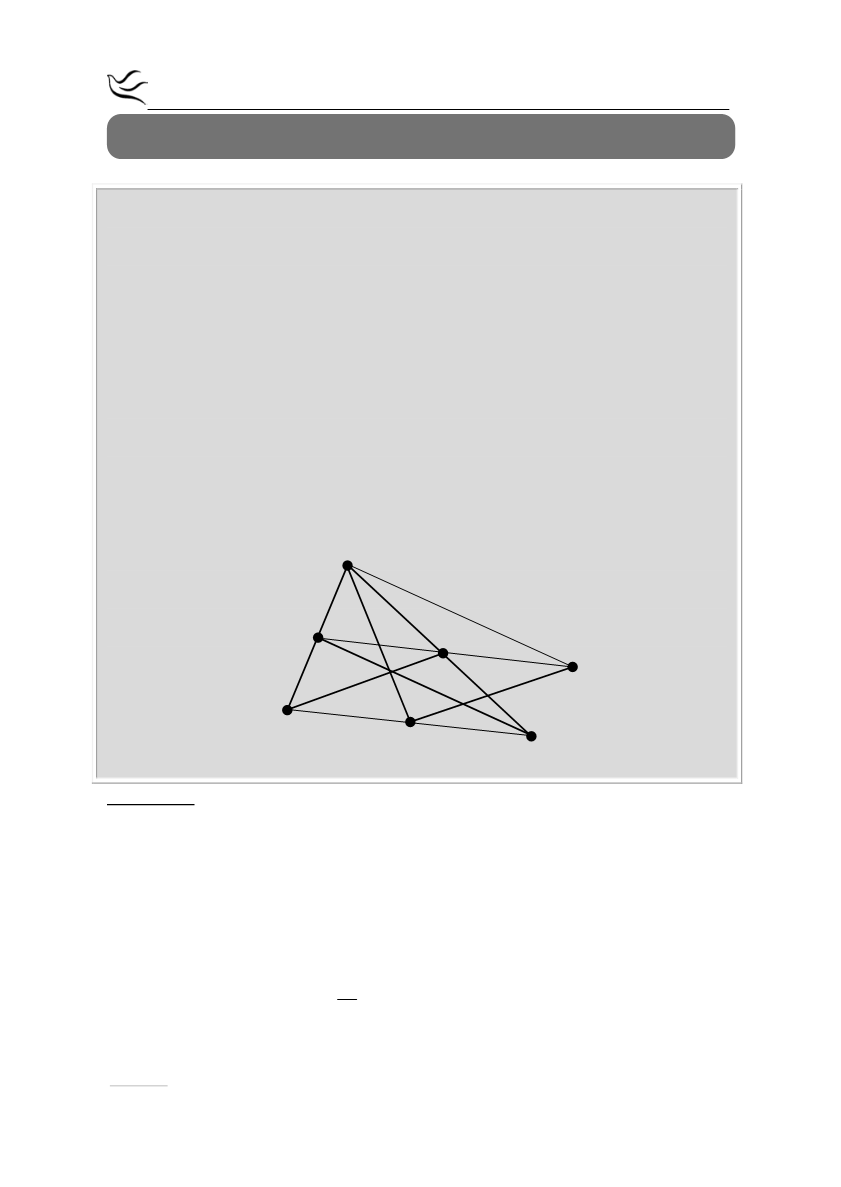
Δίνεται τρίγωνο ΑΒΓ και οι διάμεσοί του ΑΔ, ΒΕ και ΓΖ. Προεκτείνουμε το
τμήμα ΖΕ (προς το Ε) κατά τμήμα ΕΗ=ΖΕ. Να αποδείξετε ότι:
α) το τετράπλευρο ΕΗΔΒ είναι παραλληλόγραμμο
(Μονάδες 8)
β) η περίμετρος του τριγώνου ΑΔΗ είναι ίση με το άθροισμα των διαμέσων του
τριγώνου ΑΒΓ
(Μονάδες 9)
γ) οι ευθείες ΒΕ και ΔΗ τριχοτομούν το τμήμα ΖΓ.
(Μονάδες 8)
Απάντηση:
α) Στο τρίγωνο ΑΒΓ είναι
•
Ζ μέσο της ΑΒ
•
Ε μέσο της ΑΓ.
Άρα, έχουμε διαδοχικά
= ⇔ = ⇔ =
ΒΓ
ΖΕ //
ΖΕ // ΒΔ ΕΗ// ΒΔ
2
οπότε το τετράπλευρο ΕΗΔΒ είναι παραλληλόγραμμο.
ΘΕΜΑ 4593
Α
Β
Ζ
Ε
Η
Δ
Γ
166









