Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
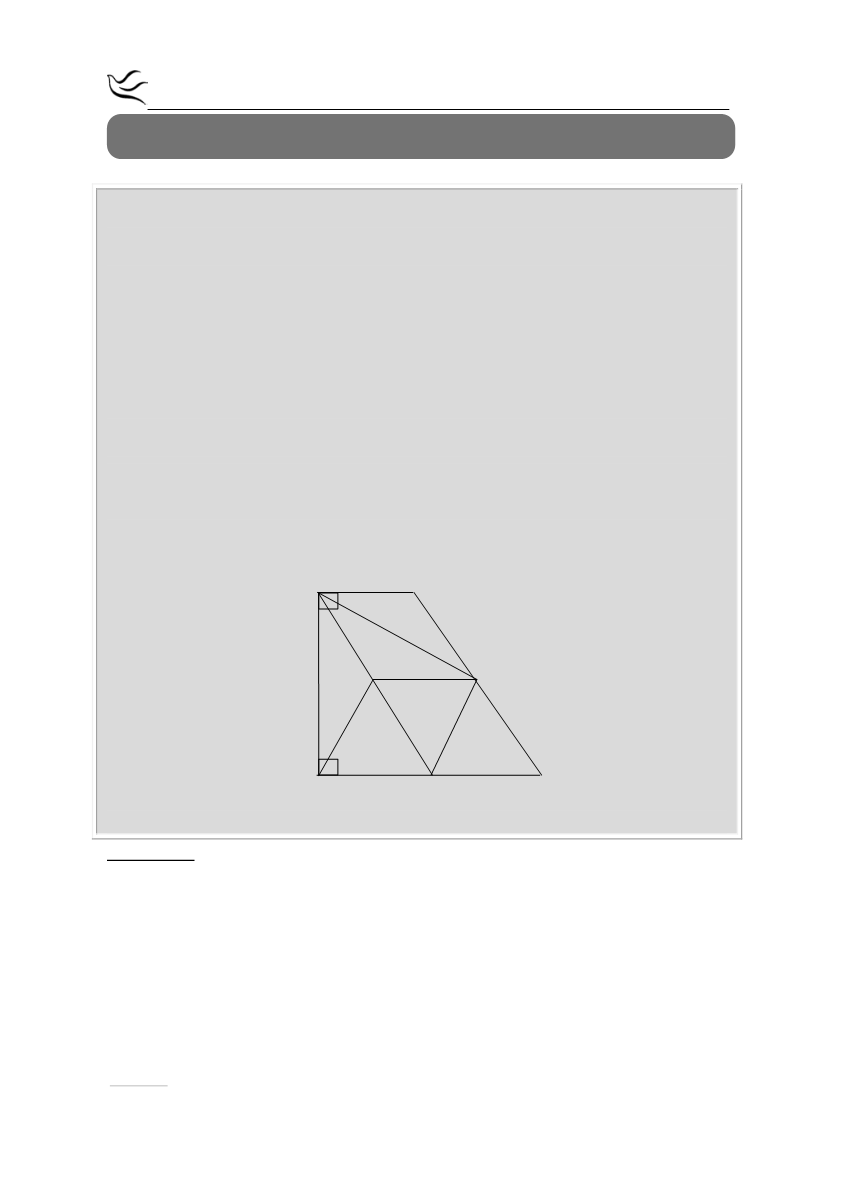
Δίνεται ορθογώνιο τραπέζιο ΑΒΓΔ (
= =
0
Α Δ 90
) με ΒΓ = ΓΔ = 2ΑΒ και Κ, Λ τα
μέσα των ΒΓ και ΓΔ. Η παράλληλη από το Κ προς την ΑΒ τέμνει την ΑΛ στο Ζ.
Να αποδείξετε ότι:
α) ΒΓ = 2ΔΖ
(Μονάδες 8)
β) το τετράπλευρο ΖΚΓΛ είναι ρόμβος
(Μονάδες 9)
γ)
=
0
ΑΚΛ 90
.
(Μονάδες 8)
Απάντηση:
α) Είναι
= ⇔ = ⇔ =
ΓΔ 2ΑΒ 2ΓΛ 2ΑΒ ΓΛ ΑΒ
και επειδή ΓΔ//ΑΒ είναι και ΓΛ//ΑΒ.
Δηλαδή το τετράπλευρο ΑΒΓΛ έχει δύο απέναντι πλευρές του ίσες και
παράλληλες άρα, είναι παραλληλόγραμμο οπότε ισχύει ΑΛ//=ΒΓ (1).
Α
Β
Γ
Λ
Δ
Ζ
Κ
ΘΕΜΑ 4599
168









