Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Άρα, ΑΜ=ΜΓ οπότε το τρίγωνο ΑΜΓ είναι ισοσκελές με
= =
0
ΜΑΓ Γ 30
.
Ακόμη,
+ = ⇔
ΒΑΜ ΜΑΓ ΒΑΓ
+ = ⇔
0
0
ΒΑΜ 30 90
=
0
ΒΑΜ 60
.
Είναι όμως και ΑΜ=ΜΒ άρα, το τρίγωνο ΜΑΒ είναι ισοσκελές με
= =
0
ΒΑΜ ΒΜΑ 60
οπότε θα είναι
+ = ⇔
0
ΑΒΜ 2ΒΑΜ 180
+ = ⇔
0
0
ΑΒΜ 120 180
=
0
ΑΒΜ 60
(1)
δηλαδή το τρίγωνο ΜΑΒ είναι ισόπλευρο με ΒΑ=ΒΜ=ΑΜ (2).
Επιπλέον, αφού το Ε ανήκει στη μεσοκάθετο της πλευράς ΒΓ θα είναι ΕΒ=ΕΓ (3)
δηλαδή και το τρίγωνο ΕΒΓ είναι ισοσκελές με
= =
0
ΕΒΓ Γ 30
(4).
Έτσι, επειδή
+ = =
ΑΒΕ ΕΒΓ ΑΒΓ ΑΒΜ
λόγω των σχέσεων (1) και (4) παίρνουμε
+ = ⇔
0
0
ΑΒΕ 30 60
=
0
ΑΒΕ 30
δηλαδή
=
ΑΒΕ ΕΒΓ
άρα, η ΒΕ είναι διχοτόμος της γωνίας
Β
.
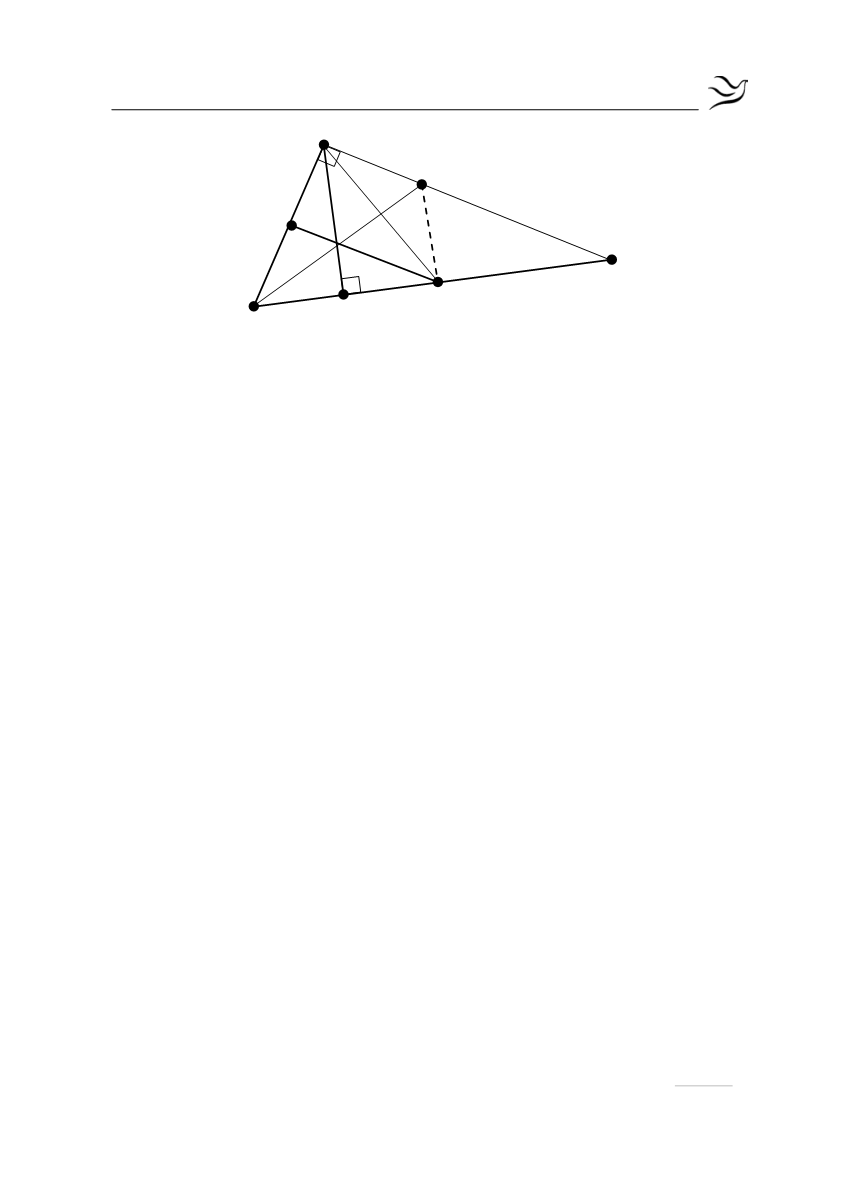
Α
Ν
Η
Μ
Β
Δ
Ε
Γ
●
181









