Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
= =
0
ΑΒΔ ΕΡΒ 60
.
Επομένως, τα τρίγωνα ΑΒΔ και ΡΕΒ έχουν δύο γωνίες τους ίσες με αποτέλεσμα
να έχουν και τις τρίτες γωνίες τους ίσες δηλαδή
=
ΔΑΒ ΕΒΡ
.
Συνεπώς, τα τρίγωνα ΑΒΔ και ΡΕB είναι ίσα γιατί
•
=
ΔΑΒ ΕΒΡ
•
ΑΒ=ΒΡ ως πλευρές ισοπλεύρου τριγώνου
•
=
ΑΒΔ ΕΡΒ
.
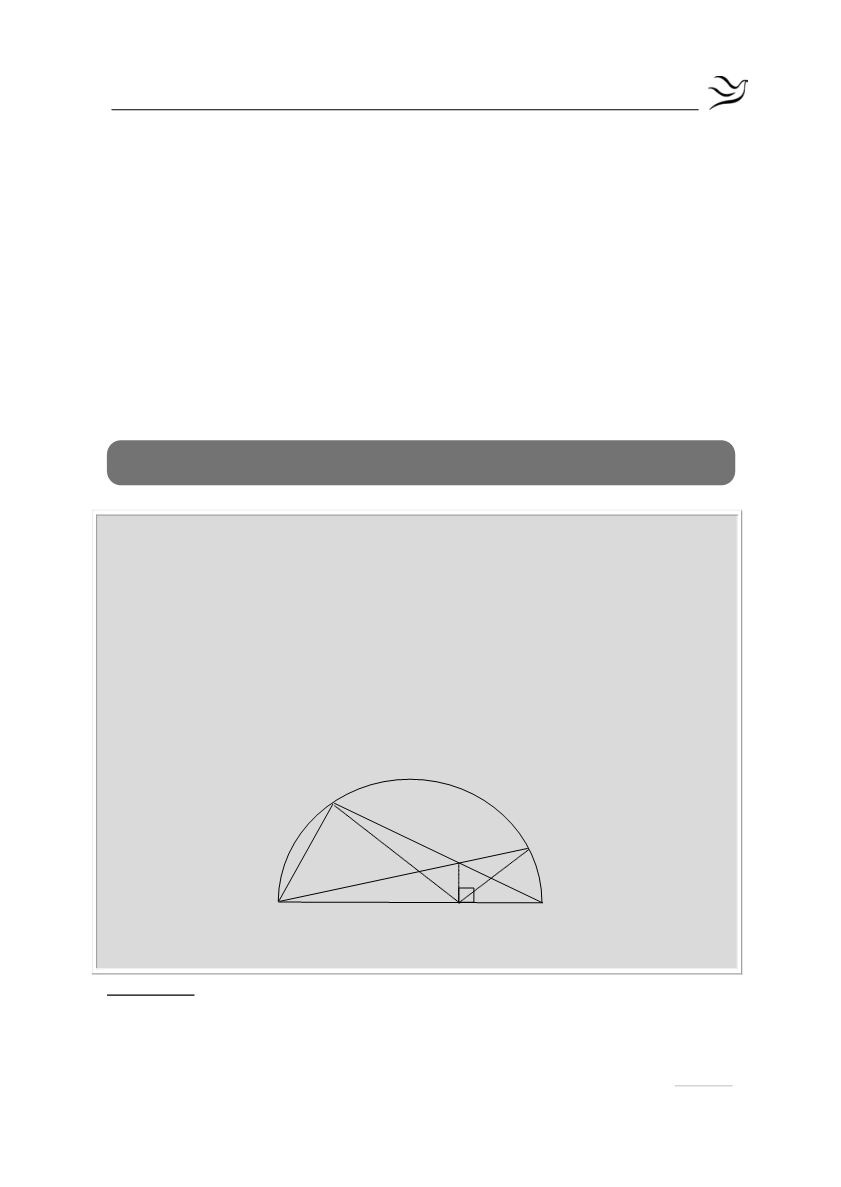
Δίνεται ημικύκλιο διαμέτρου ΑΒ και δύο χορδές του ΑΓ και ΒΔ, οι οποίες
τέμνονται στο σημείο Ε. Φέρουμε
⊥
ΕΖ ΑΒ
. Να αποδείξετε ότι:
α) οι γωνίες
ΔΑΓ
και
ΔΒΓ
είναι ίσες
(Μονάδες 7)
β) τα τετράπλευρα ΑΔΕΖ και ΕΖΒΓ είναι εγγράψιμα
(Μονάδες 9)
γ) η ΕΖ είναι διχοτόμος της γωνίας
ΔΖΓ
.
(Μονάδες 9)
Απάντηση:
α) Είναι
=
ΔΑΓ ΔΒΓ
Ζ
Δ
Γ
Ε
Α
•
Β
Ο
ΘΕΜΑ 3771
139









