Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Όμως οι διαγώνιοι του ορθογωνίου είναι ίσες και διχοτομούνται οπότε
ΑΟ=ΟΔ
Άρα, το τρίγωνο ΑΟΔ είναι ισοσκελές με
=
ΟΑΔ ΟΔΑ
επομένως, θα είναι και
= =
0
ΟΔΑ ΒΔΕ 60
.
Ακόμη, έχουμε διαδοχικά ότι
= = = =
ΒΔ ΑΓ 2ΒΓ 2ΑΔ ΔΕ
άρα, το τρίγωνο ΒΔΕ είναι ισοσκελές με
=
ΔΒΕ ΔΕΒ
και
=
0
ΒΔΕ 60
οπότε θα είναι
+ = ⇔
0
0
60 2ΔΒΕ 180
= ⇔
0
2ΔΒΕ 120
=
0
ΔΒΕ 60
δηλαδή το τρίγωνο ΕΒΔ είναι ισόπλευρο.
β) Επειδή ΔΟ=ΟΒ στο ισόπλευρο τρίγωνο ΕΒΔ η ΕΟ είναι διάμεσος άρα, θα
είναι και ύψος. Ακόμη, στο ίδιο τρίγωνο και η ΒΑ είναι ύψος αφού
⊥
ΒΑ ΕΔ
.
Έτσι το Ζ είναι το ορθόκεντρο του τριγώνου ΕΒΔ άρα, η ΔΖ θα είναι ο φορέας
του τρίτου ύψους οπότε θα είναι
⊥
ΔΖ ΕΒ
.
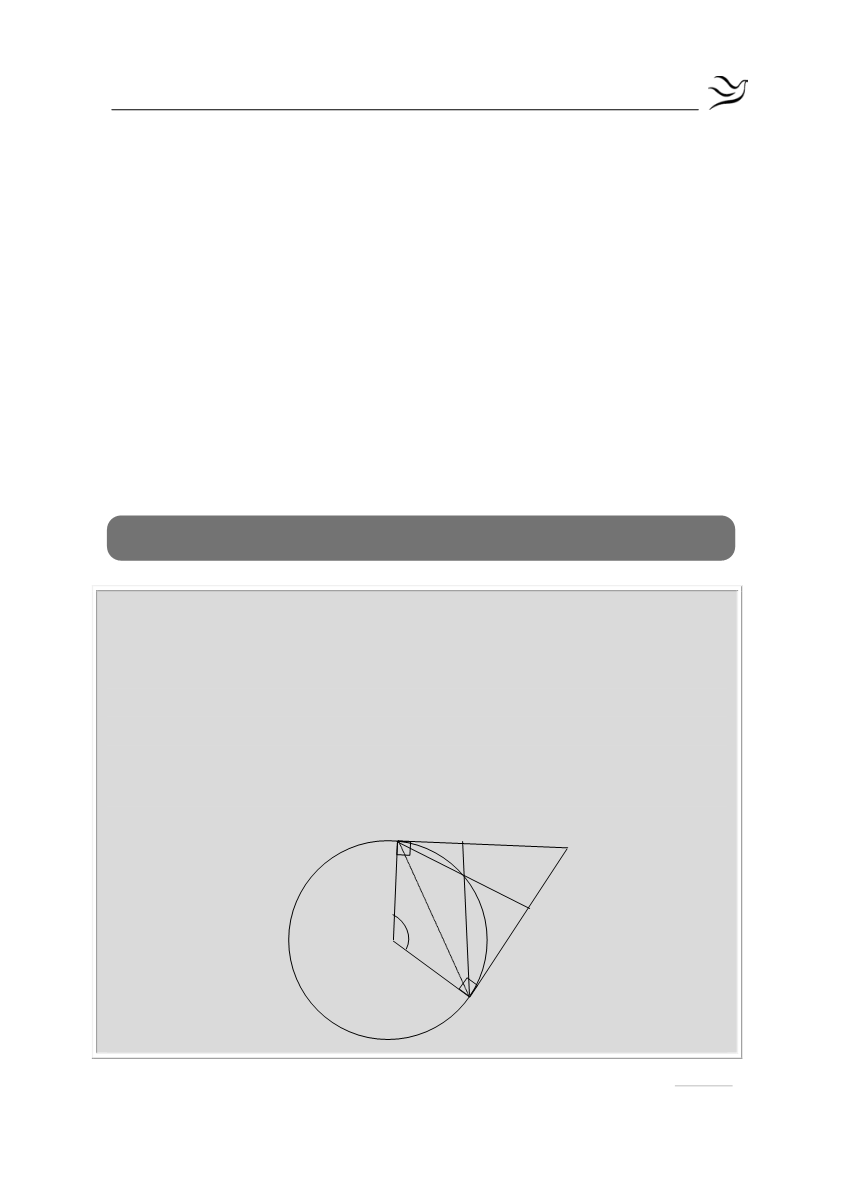
Δίνεται κύκλος (Ο, R) και μια επίκεντρη γωνία του
ΑΟΒ
ίση με 120
0
. Οι
εφαπτόμενες του κύκλου στα σημεία Α και Β τέμνονται στο σημείο Ρ.
Θεωρούμε σημείο Μ του τόξου ΑΒ και φέρουμε τις χορδές ΑΜ και ΒΜ, οι
οποίες προεκτεινόμενες τέμνουν τις ΡΒ και ΡΑ και στα σημεία Δ και Ε
αντίστοιχα. Να αποδείξετε ότι:
α) το τρίγωνο ΑΡΒ είναι ισόπλευρο (Μονάδες 8)
β)
+ =
0
ΜΑΒ ΜΒΑ 60
(Μονάδες 8)
γ) τα τρίγωνα ΑΒΔ και ΡΕB είναι ίσα. (Μονάδες 9)
B
A
120
0
Ρ
Ο
Ε
M
Δ
ΘΕΜΑ 3767
137









