Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
θα είναι
⊥
ΑΝ ΒΓ
άρα, οι διαγώνιοι του παραλληλογράμμου ΑΒΝΓ τέμνονται
κάθετα. οπότε το τετράπλευρο ΑΒΝΓ είναι ρόμβος.
β) Παρατηρούμε ότι στο τρίγωνο ΑΔΝ η ΔΜ είναι ύψος και διάμεσος οπότε το
τρίγωνο ΑΔΝ είναι ισοσκελές.
γ) Στο τρίγωνο ΑΔΝ η ΔΜ είναι διάμεσος οπότε για να είναι το Γ το βαρύκεντρο
του τριγώνου θα πρέπει να είναι
=
2 ΔΓ ΔΜ
3
. Πράγματι έχουμε διαδοχικά
= − = − = −
ΒΓ
ΔΓ
ΔΓ ΔΜ ΓΜ ΔΜ ΔΜ
2
2
.
Άρα,
= − ⇔
2ΔΓ 2ΔΜ ΔΓ
= ⇔
3ΔΓ 2ΔΜ
=
2 ΔΓ ΔΜ
3
.
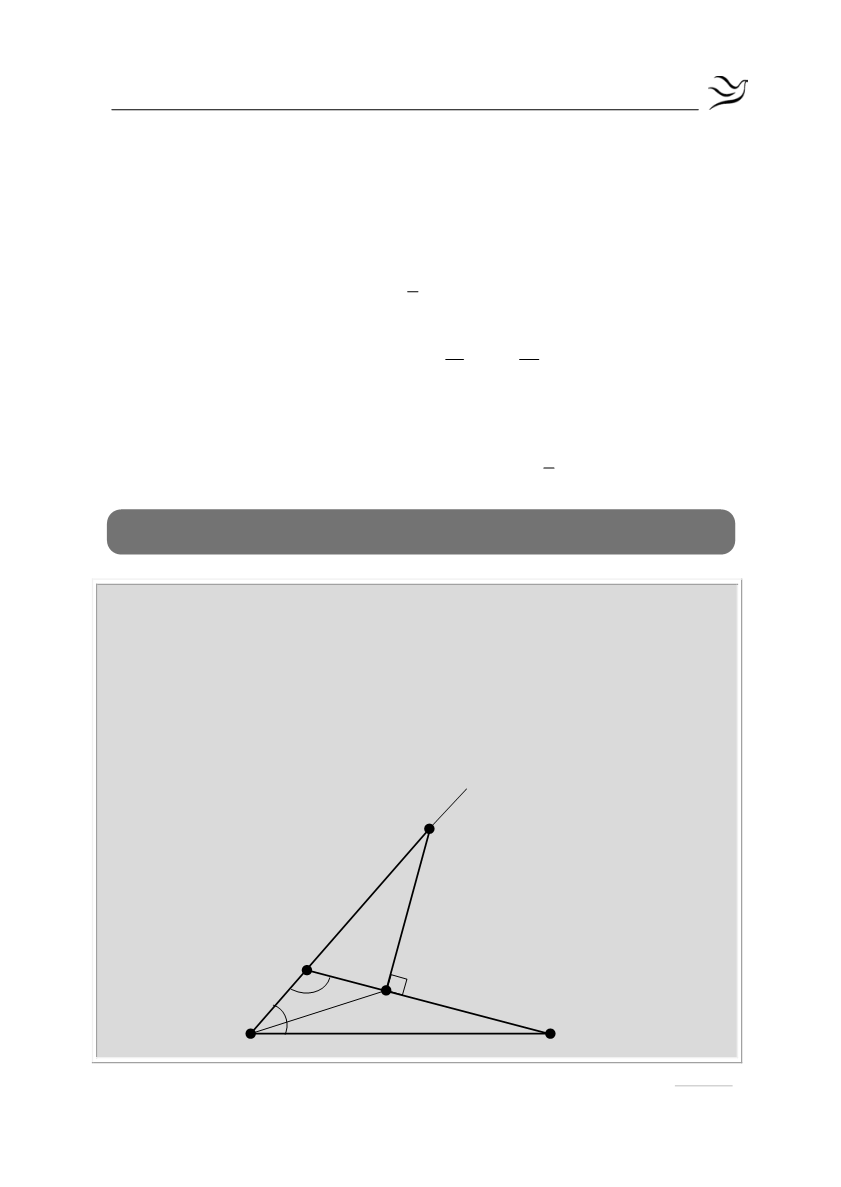
Δίνεται τρίγωνο ΑΒΓ με γωνία
Α
ίση με 120
0
και γωνία
Β
ίση με 45
0
. Στην
προέκταση της ΒΑ προς το Α, παίρνουμε τμήμα ΑΔ = 2ΑΒ. Από το Δ φέρουμε
την κάθετη στην ΑΓ που την τέμνει στο σημείο Κ. Να αποδείξετε ότι:
α) η γωνία
ΑΔΚ
είναι ίση με 30
0
(Μονάδες 6)
β) το τρίγωνο ΚΑΒ είναι ισοσκελές (Μονάδες 6)
γ) αν Ζ το μέσο της ΔΑ, τότε
=
0
ΖΚΒ 90
(Μονάδες 6)
δ) το σημείο Κ ανήκει στη μεσοκάθετο του τμήματος ΒΔ. (Μονάδες 7)
120
0
Γ
Δ
A
K
B
45
0
ΘΕΜΑ 3747
133









