Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Δίνεται τρίγωνο ΑΒΓ με ΑΒ<ΑΓ. Έστω Αχ η εξωτερική διχοτόμος της γωνίας
Α
.
α) Να αποδείξετε ότι:
i.
−
+ = +
εξ
0
εξ
Α
Γ Β
Β 180
2
2
, όπου
εξ
Α
,
εξ
Β
, οι εξωτερικές γωνίες των
Α
,
Β
(Μονάδες 10)
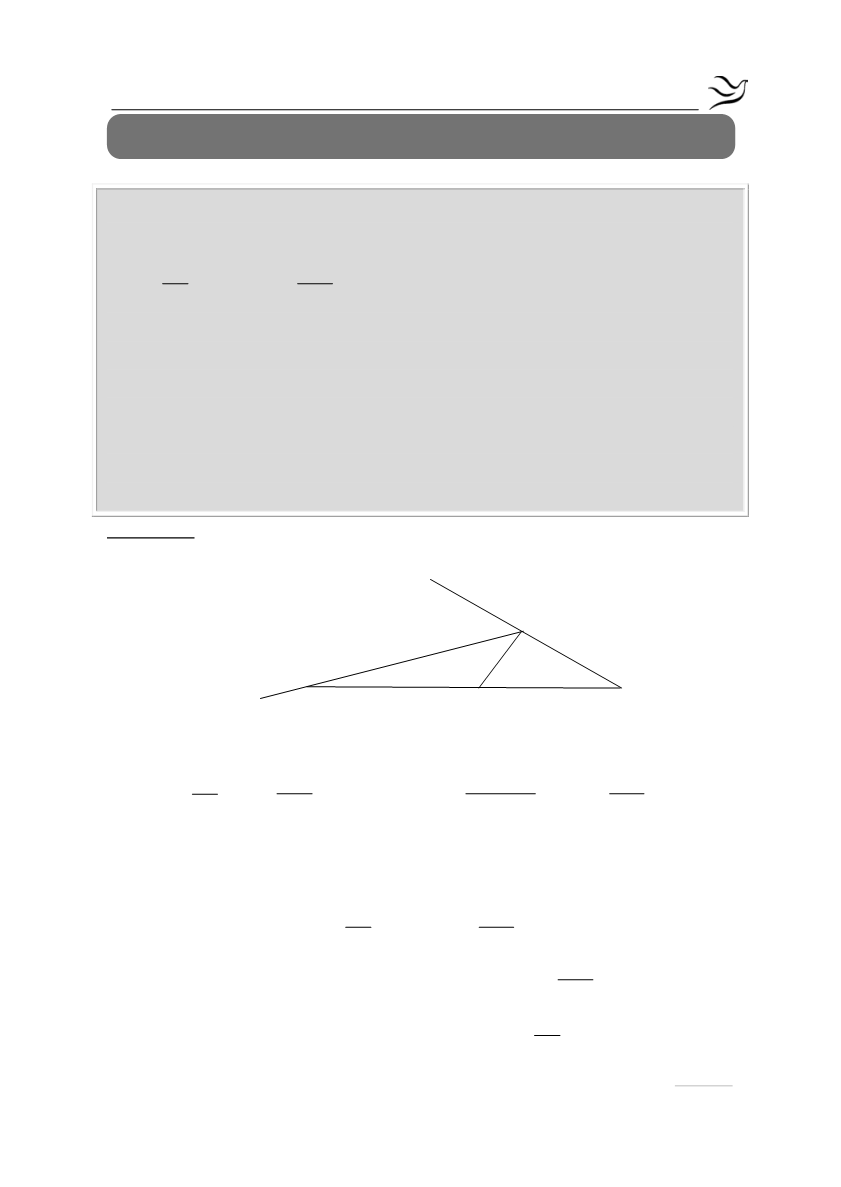
ii. η εξωτερική διχοτόμος της γωνίας
Α
τέμνει την προέκταση της πλευράς
ΓΒ (προς το μέρος του Β) σε σημείο Ζ .
(Μονάδες 8)
β) Αν το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α και
=
0
ΑΖΒ 15
, να αποδείξετε ότι
ΒΓ=2ΑΒ.
(Μονάδες 7)
Απάντηση:
α) i.
Είναι
+ =
εξ
εξ
Α
Β
2
+
+ − =
0
Β Γ 180 Β
2
+ −
+
=
0
Β Γ 2Β
180
2
−
+
0
Γ Β
180
2
.
ii. Αρκεί να αποδείξουμε ότι
+ <
0
1 1
Α B 180
.
Πράγματι είναι
−
+ = + = − <
εξ
0
0
1 1
εξ
Α
Β Γ
Α B
Β 180
180
2
2
και αυτό γιατί στο τρίγωνο ΑΒΓ είναι ΑΒ<ΑΓ άρα,
−
< ⇔ >
Β Γ
Γ Β
0
2
.
β) Αν το τρίγωνο ΑΒΓ είναι ορθογώνιο στο Α τότε
= =
εξ
0
1
Α
Α
45
2
οπότε
Α
Β
Γ
Ζ
x
1
1
ΘΕΜΑ 3735
131









