Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Απάντηση:
α) Τα εφαπτόμενα τμήματα ΜΑ και ΜΒ είναι κάθετα στα άκρα Α και Β των
ακτίνων ΟΑ και ΟΒ του κύκλου. Άρα,
= =
0
MAO MBO 90
.
Συνεπώς, το τετράπλευρο ΑΜΒΟ έχει δύο απέναντι γωνίες παραπληρωματικές
άρα, είναι εγγράψιμο σε κύκλο.
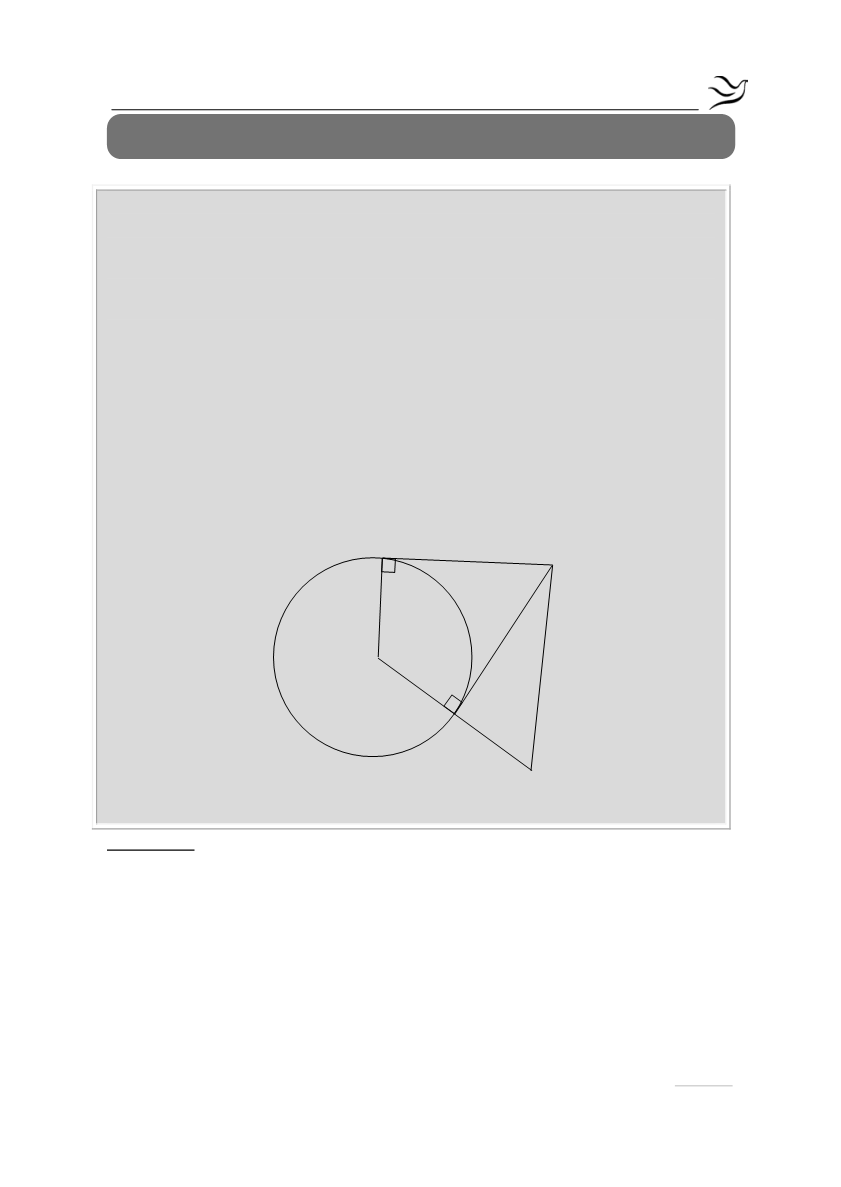
Δίνεται κύκλος (Ο, ρ) και σημείο Μ εξωτερικό του. Από το Μ φέρνουμε τα
εφαπτόμενα τμήματα ΜΑ και ΜΒ του κύκλου και έστω ότι Γ είναι το
συμμετρικό σημείο του Ο ως προς την ευθεία ΜΒ.
α) Να αποδείξετε ότι το τετράπλευρο ΑΜΒΟ είναι εγγράψιμο σε κύκλο.
(Μονάδες 9)
β) Να προσδιορίσετε το κέντρο Λ του περιγγεγραμμένου κύκλου του
τετραπλεύρου ΑΜΒΟ και να αιτιολογήσετε την απάντησή σας.
(Μονάδες 9)
γ) Να αποδείξετε ότι ΒΛ//ΜΓ.
(Μονάδες 7)
B
A
Γ
M
Ο
ΘΕΜΑ 3731
127









