Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Επομένως, θα είναι ΔΑ//ΓΒ.
Επιπλέον, επειδή το Ε δεν είναι το μέσο του τόξου
ΑΒ
θα είναι
≠
0
1
Ο 90
και
αφού
=
0
ΔΕΟ 90
οι ΔΓ και ΑΒ δεν είναι παράλληλες.
Συνεπώς, το τετράπλευρο ΑΒΓΔ έχει μόνο δυο πλευρές παράλληλες άρα, είναι
τραπέζιο.
ii. Είναι ΔΕ=ΔΑ ως εφαπτόμενα τμήματα και ομοίως ΓΕ=ΓΒ.
Άρα,
+ = + ⇔
ΓΕ ΕΔ ΒΓ ΑΔ
= +
ΓΔ ΑΔ ΒΓ
.
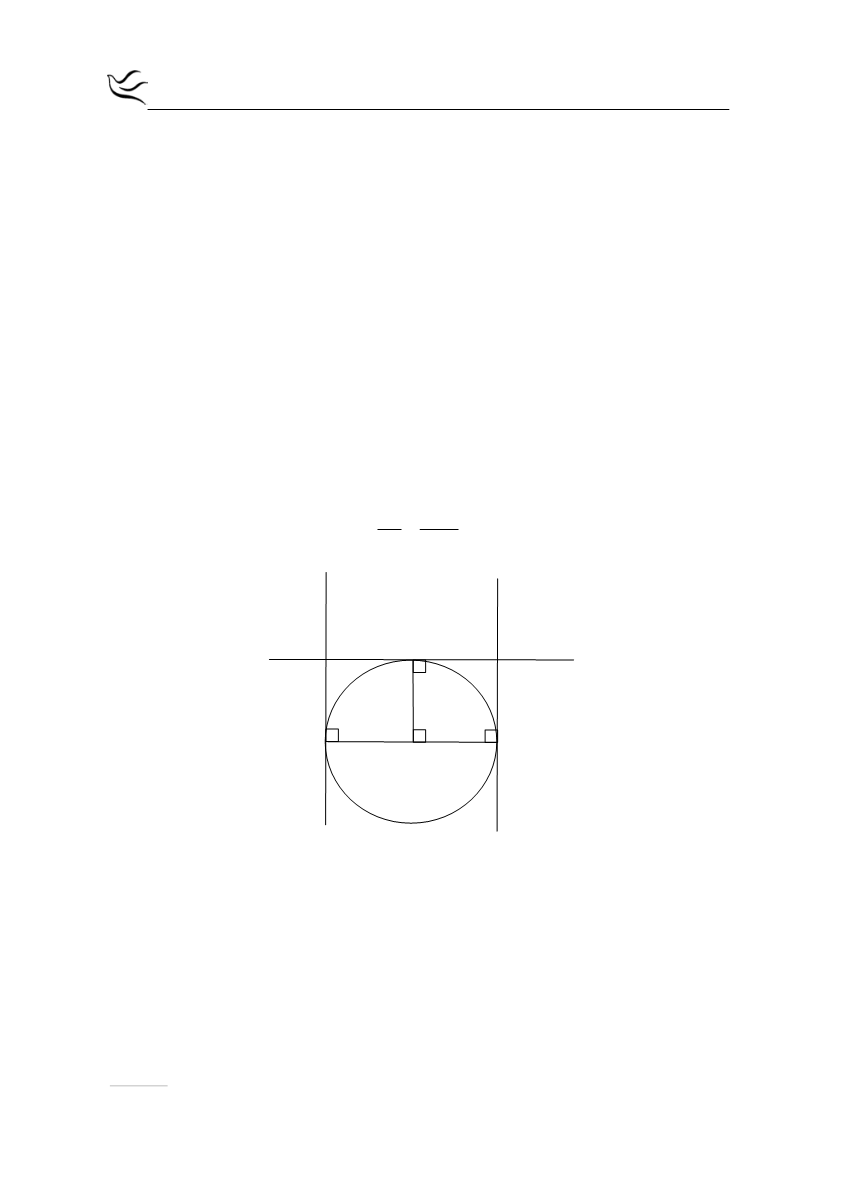
β) Αν το σημείο Ε βρίσκεται στο μέσον του τόξου ΑΒ είναι
= = =
0
0
1
ΑΒ 180
Ο
90
2 2
.
Ακόμη, η εφαπτόμενη ε
2
είναι κάθετη στη διάμετρο ΑΒ στο σημείο Β άρα
=
0
Β 90
. Ομοίως και
=
0
Ε 90
. Άρα, το τετράπλευρο ΟΒΓΕ είναι ορθογώνιο και
επειδή ΟΒ=ΟΕ=R θα είναι τετράγωνο με ΒΓ=R και
=
0
Γ 90
.
Άρα, το τετράπλευρο ΑΔΓΒ έχει τρεις γωνίες ορθές οπότε είναι ορθογώνιο και η
περίμετρός του είναι
= + = ⋅ + = + =
Π 2ΑΒ 2ΒΓ 2 2R 2R 4R 2R 6R
.
ε
Β
Α
E
Ο
Δ
ε
1
Γ
ε
2
1
122









