Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Απάντηση:
α) i.
Οι εφαπτόμενες ε
1
, ε
2
είναι κάθετες στη διάμετρο ΑΒ στα σημεία Α και Β. Άρα,
⊥
ΔΑ ΑΒ
και
⊥
ΓΒ ΑΒ
.
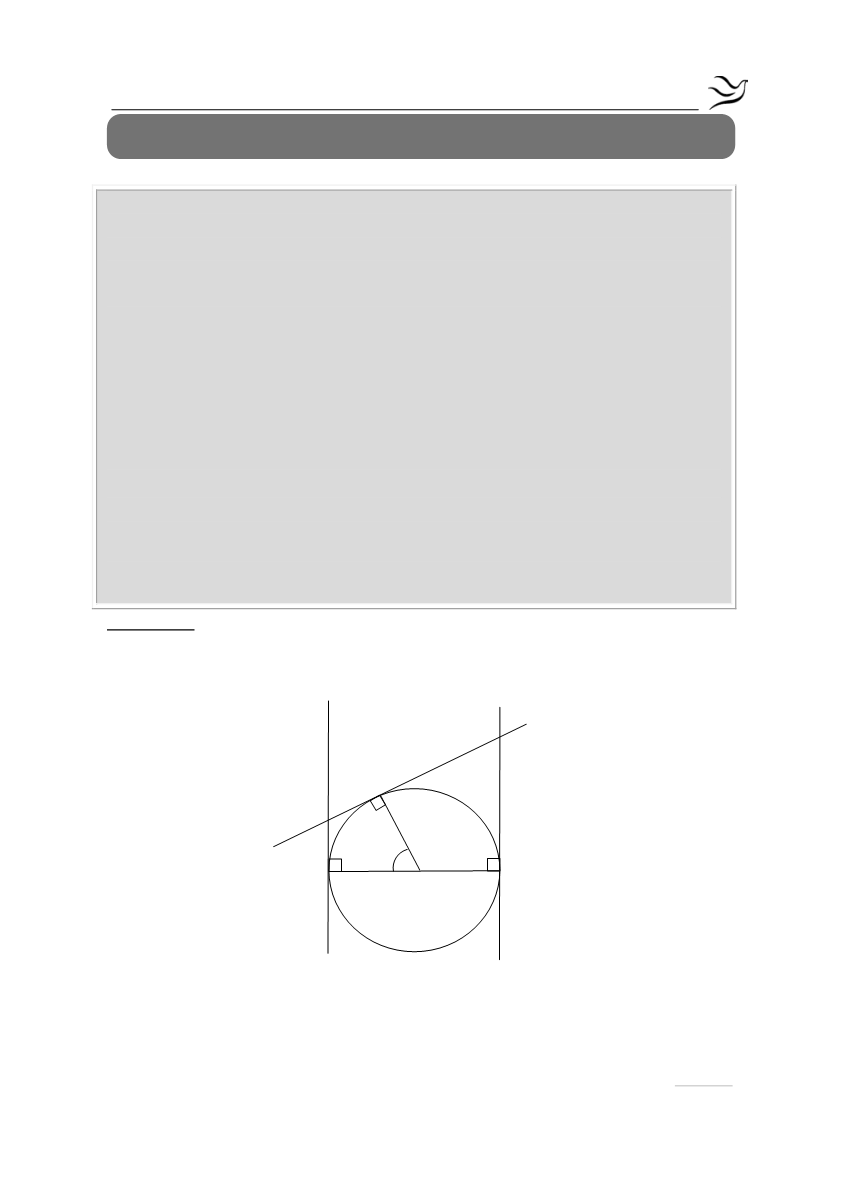
Δίνεται κύκλος (Ο, R) με διάμετρο ΑΒ και δυο ευθείες ε
1
, ε
2
εφαπτόμενες του
κύκλου στα άκρα της διαμέτρου ΑΒ. Έστω ότι μια τρίτη ευθεία ε εφάπτεται
του κύκλου σ' ένα σημείο του Ε και τέμνει τις ε
1
και ε
2
στα Δ και Γ αντίστοιχα.
α) Αν το σημείο Ε δεν είναι το μέσο του τόξου
ΑΒ
, να αποδείξετε ότι:
i. το τετράπλευρο ΑΒΓΔ είναι τραπέζιο
(Μονάδες 8)
ii. ΓΔ=ΑΔ+ΒΓ.
(Μονάδες 8)
β) Αν το σημείο Ε βρίσκεται στο μέσο του τόξου
ΑΒ
να αποδείξετε ότι το
τετράπλευρο ΑΔΓΒ είναι ορθογώνιο. Στην περίπτωση αυτή να εκφράσετε την
περίμετρο του ορθογωνίου ΑΔΓΒ ως συνάρτηση της ακτίνας R του κύκλου.
(Μονάδες 9)
Β
Α
E
Ο
Δ
1
ε
1
ε
Γ
ε
2
ΘΕΜΑ 3724
121









