Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
= + = + =
0
0
0
1
ΖΑΓ Α Α 45 90 135
οπότε στο τρίγωνο ΖΑΓ είναι
+ + = ⇔
0
ΑΖΓ ΖΑΓ ΖΓΑ 180
+ + = ⇔
0
0
0
15 135 ΖΓΑ 180
= − ⇔
0
0
ΖΓΑ 180 150
=
0
ΖΓΑ 30
.
Επομένως, στο ορθογώνιο τρίγωνο ΑΒΓ θα είναι
=
0
ΒΓΑ 30
οπότε θα ισχύει
= ⇔
ΒΓ ΑΒ
2
=
ΒΓ 2ΑΒ
.
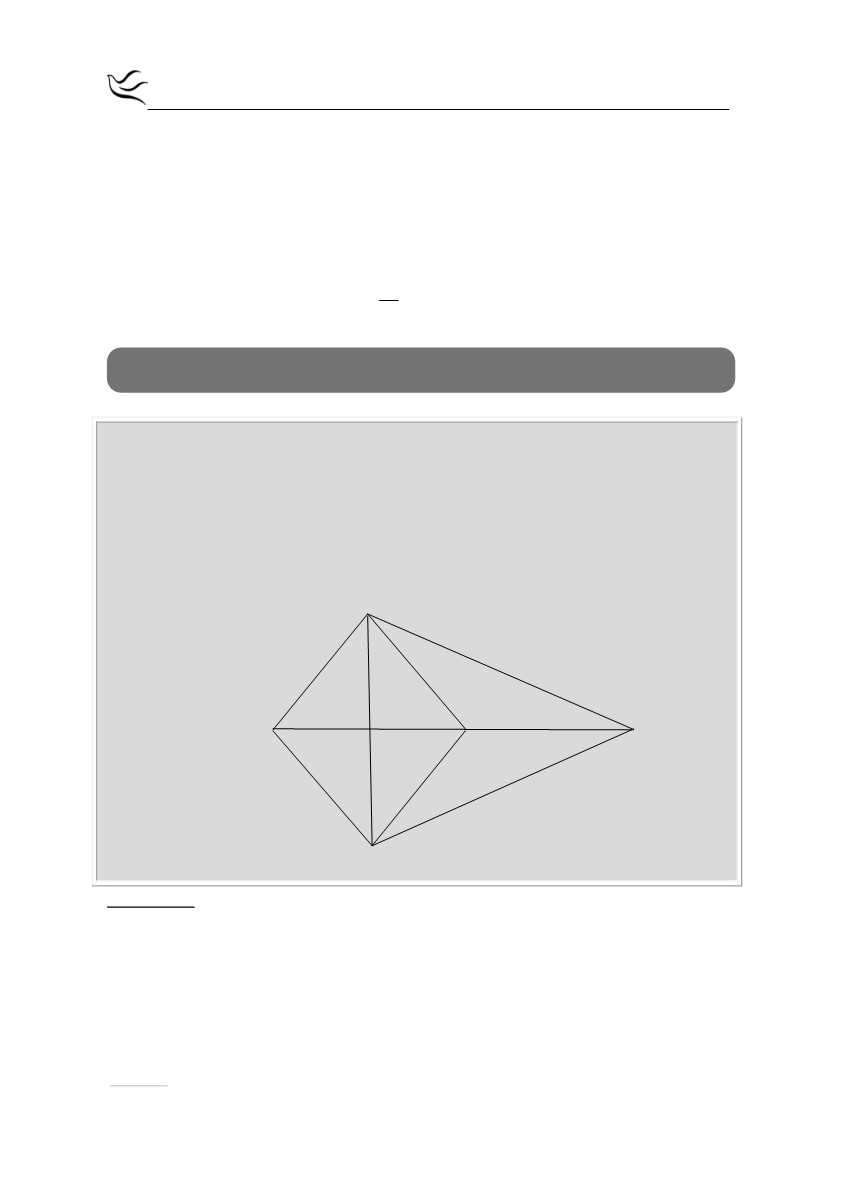
Δίνεται ισοσκελές τρίγωνο ΑΒΓ (ΑΒ=ΑΓ) και ΑΜ το ύψος του στην πλευρά ΒΓ.
Στην προέκταση του ΑΜ θεωρούμε τμήμα ΜΝ=ΑΜ. Στην προέκταση του ΒΓ
προς το μέρος του Γ θεωρούμε τμήμα ΓΔ =ΒΓ. Να αποδείξετε ότι:
α) το τετράπλευρο ΑΒΝΓ είναι ρόμβος (Μονάδες 8)
β) το τρίγωνο ΑΔΝ είναι ισοσκελές (Μονάδες 8)
γ) το σημείο Γ είναι το βαρύκεντρο του τριγώνου ΑΔΝ. (Μονάδες 9)
Απάντηση:
α) Στο ισοσκελές τρίγωνο ΑΒΓ αφού ΑΜ το ύψος του προς τη βάση του ΒΓ θα
είναι και διάμεσός του. Θα είναι δηλαδή και ΒΜ=ΜΓ (1). Ακόμη, ΑΜ=ΜΝ (2).
Από τις σχέσεις (1) και (2) συμπεραίνουμε ότι οι διαγώνιοι του τετραπλεύρου
ΑΒΝΓ διχοτομούνται άρα, το τετράπλευρο ΑΒΝΓ είναι παραλληλόγραμμο.
Ακόμη, στο ισοσκελές τρίγωνο ΑΒΓ αφού ΑΜ το ύψος του προς τη βάση του ΒΓ
Γ
Α
Β
Ν
Δ
Μ
ΘΕΜΑ 3745
132









