Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
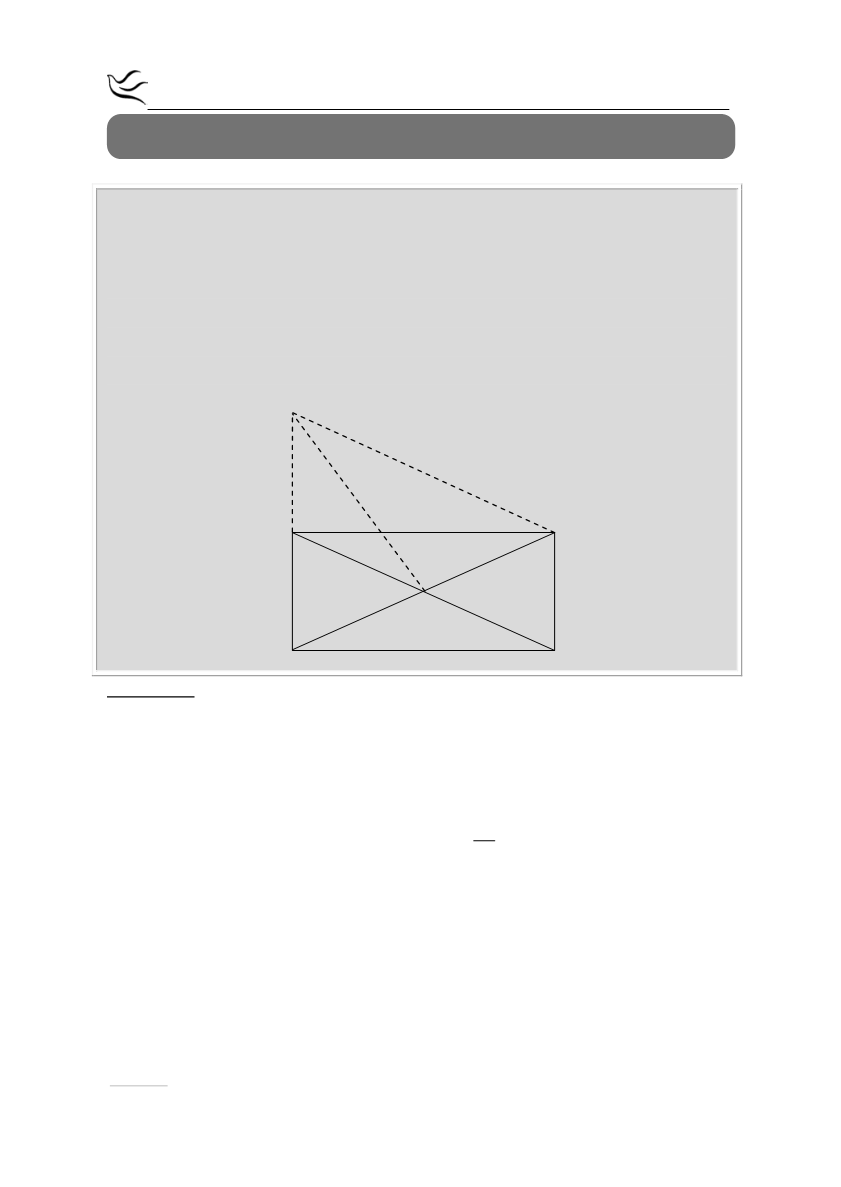
Δίνεται ορθογώνιο ΑΒΓΔ με κέντρο Ο και ΑΒ > ΒΓ, ΑΓ=2ΒΓ. Στην προέκταση της
πλευράς ΔΑ (προς το Α) παίρνουμε σημείο Ε ώστε ΔΑ=ΑΕ.
α) Να αποδείξετε ότι:
i. το τετράπλευρο ΑΕΒΓ είναι παραλληλόγραμμο (Μονάδες 8)
ii. το τρίγωνο ΕΒΔ είναι ισόπλευρο (Μονάδες 9)
β) Αν η ΕΟ τέμνει την πλευρά ΑΒ στο σημείο Ζ, να αποδείξετε ότι
⊥
ΔΖ ΕΒ
.
(Μονάδες 8)
Απάντηση:
α) i. Επειδή ΑΒΓΔ ορθογώνιο θα είναι ΒΓ//ΑΔ άρα και ΒΓ//ΑΕ. Ακόμη, ισχύει
ΒΓ=ΑΔ=ΑΕ.
Συνεπώς, ισχύει ΒΓ//=ΑΕ άρα, το τετράπλευρο ΑΕΒΓ είναι παραλληλόγραμμο.
ii. Στο ορθογώνιο τρίγωνο ΑΒΓ είναι
= ⇔
ΑΓ 2ΒΓ
=
ΑΓ ΒΓ
2
οπότε
=
0
ΓΑΒ 30
και επειδή
+ = ⇔ = − ⇔ =
0
0
0
0
ΓΑΒ ΓΑΔ 90 ΓΑΔ 90 30 ΓΑΔ 60
θα είναι
= =
0
ΓΑΔ ΟΑΔ 60
.
Β
Ζ
Γ
A
Δ
Ε
Ο
ΘΕΜΑ 3757
136









