93
Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’ – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
2
2
2
2
ΑΒ ΑΓ
3 x 2 y
1 x
y
6x 2x 4y 12 0 y x 3 1
Το Α όμως είναι σημείο του κύκλου οπότε:
(1)
2
2
2
2
2
2
2
2
x 2 y 1 2
x 2
x 3 1 2 x 2
x 2 2
2 x 2 2 x 2 1 x 2 1 x 3 ή x 1
Αν
x 3
τότε από την (1) προκύπτει ότι
y 0
και Α(3,0) ενώ,
αν
x 1
τότε από την (1) προκύπτει ότι
y 2
και Α(1,2).
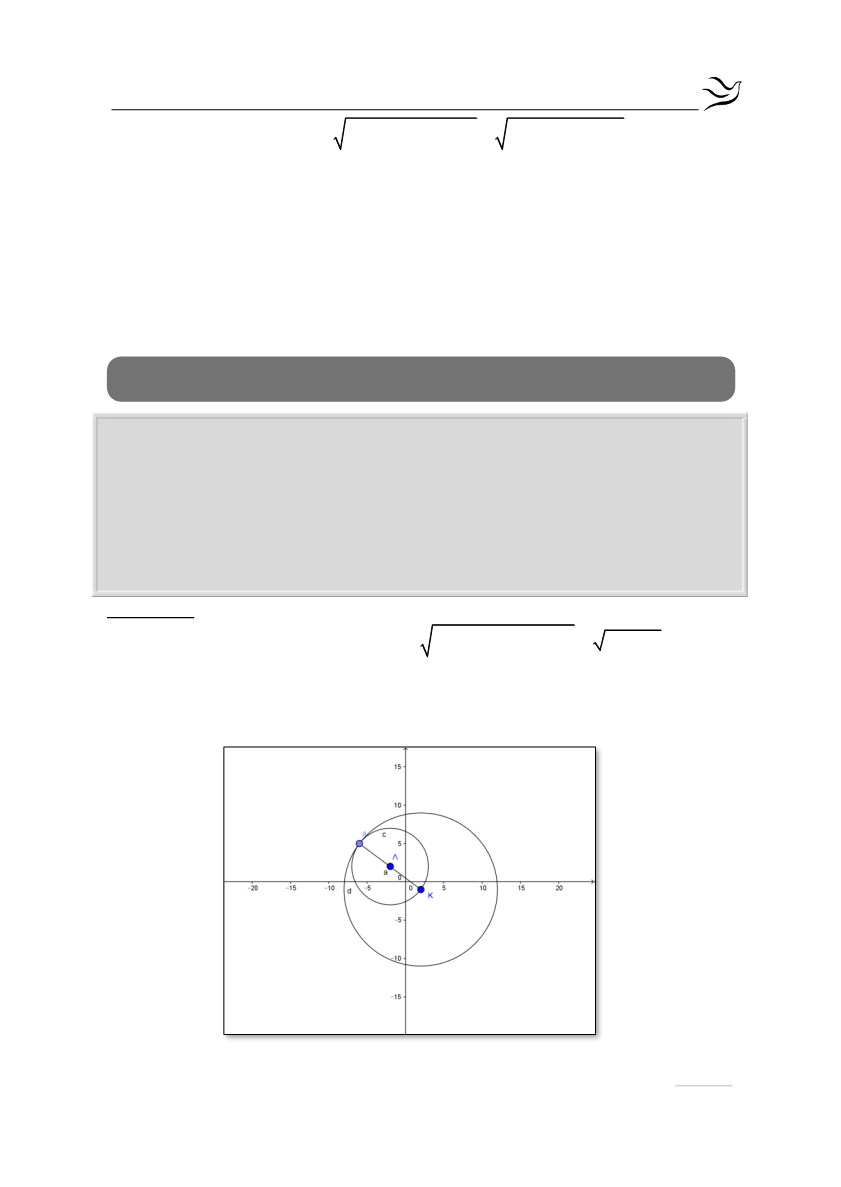
Σε καρτεσιανό επίπεδο Oxy θεωρούμε τα σημεία K(2,
1) και A(
6,5).
α.
Να αποδείξετε ότι ο κύκλος με κέντρο Κ που διέρχεται από το Α, έχει
εξίσωση
2
2
C: (x 2)
(y 1) 100
(Μονάδες 12)
β.
Να βρείτε την εξίσωση κύκλου που εφάπτεται εσωτερικά στον κύκλο C στο
σημείο Α και έχει ακτίνα ίση με το μισό της ακτίνας του C.
(Μονάδες 13)
Απάντηση:
α.
Η ακτίνα του κύκλου είναι
2
2
R
ΚΑ
6 2
5 1 64 36 10
και
η εξίσωσή του είναι:
2
2
C: (x 2) (y 1) 100
.
β.
Επειδή ο ζητούμενος κύκλος
΄
έχει ακτίνα ίση με το μισό της ακτίνας του
και εφάπτεται εσωτερικά με αυτόν, το κέντρο του είναι το μέσο Λ του ΚΑ.
ΘΕΜΑ 2– 22534









