Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’ – Εκδόσεις ΜΠΑΧΑΡΑΚΗ

Σε καρτεσιανό επίπεδο Oxy θεωρούμε κύκλο C που διέρχεται από το σημείο

Α(3,10) και έχει κέντρο το Κ(4,8).

α.

Να αποδείξετε ότι

  



C: (x 4)

(y 8) 5

, και έπειτα να βρείτε την εξίσωση

της ευθείας ε που διέρχεται από τα σημεία O και K.

(Μονάδες 13)

β.

Από τα σημεία του κύκλου C να βρείτε τις συντεταγμένες:

του σημείου που απέχει τη μικρότερη απόσταση από την αρχή των

αξόνων.

(Μονάδες 6)

ii.

του σημείου που απέχει τη μεγαλύτερη απόσταση από την αρχή των

αξόνων.

(Μονάδες 6)

Απάντηση:

α.

Αφού ο κύκλος έχει κέντρο το σημείο

(4,8)

θα έχει εξίσωση:









2 2

x 4 y 8 ρ



  

και διέρχεται από το σημείο





Α 3,10

οπότε:









2 2

3 4 10 8

ρ 5 ρ 5

 

     

Επομένως ο κύκλος έχει εξίσωση:



 



x 4 y 8

  



Η εξίσωση της ευθείας που διέρχεται από τα Ο και Κ είναι της μορφής

λx



και οι συντεταγμένες του Κ την επαληθεύουν. Άρα

8 4λ λ 2

  

Επομένως

 

ΟΚ : y 2x



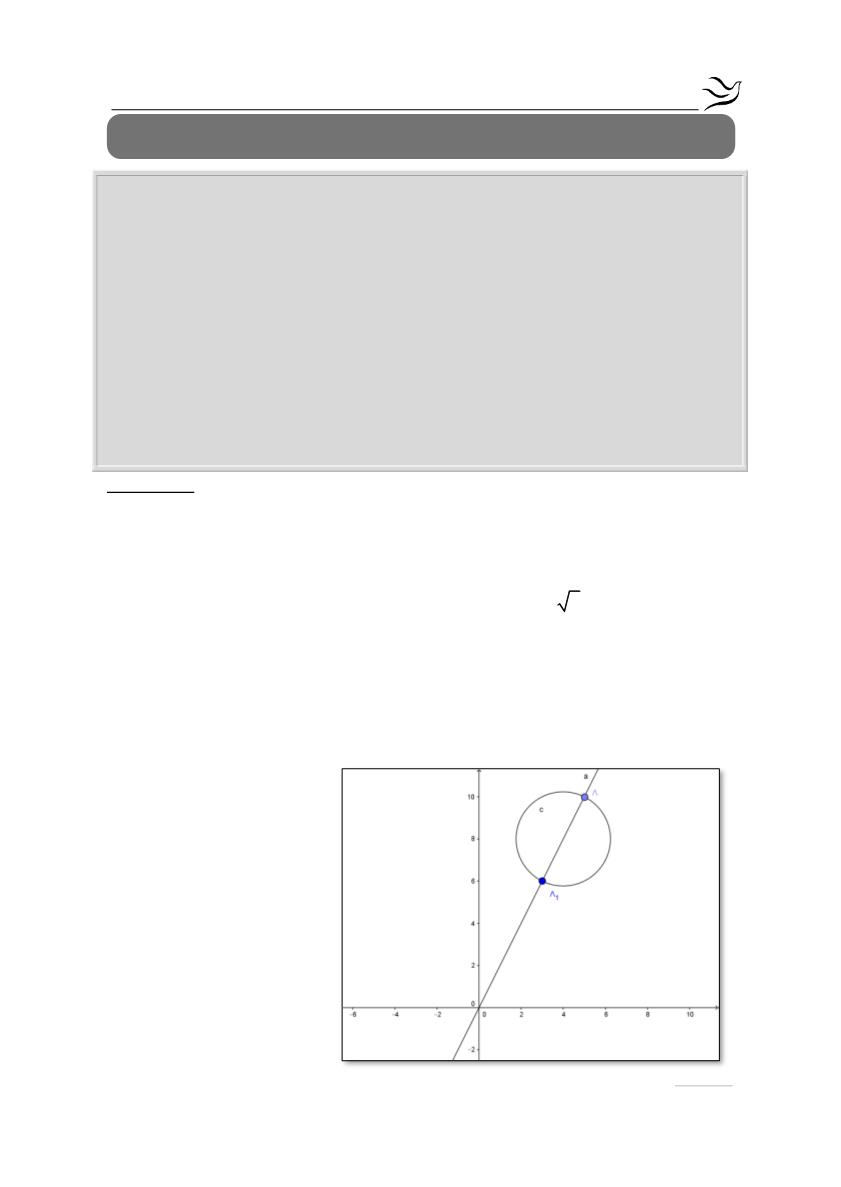
β. i.ii.

Η (ΟΚ) τέμνει τον

κύκλο και είναι

διάμετρός του. Άρα για

να βρούμε τα

σημεία του κύκλου που

απέχουν την μικρότερη

και την μεγαλύτερη

απόσταση από την αρχή

των αξόνων λύνουμε το

σύστημα:

ΘΕΜΑ 2 – 22508