Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

86 / 130

85
Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’ – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
   
1 2 2 2 2 2
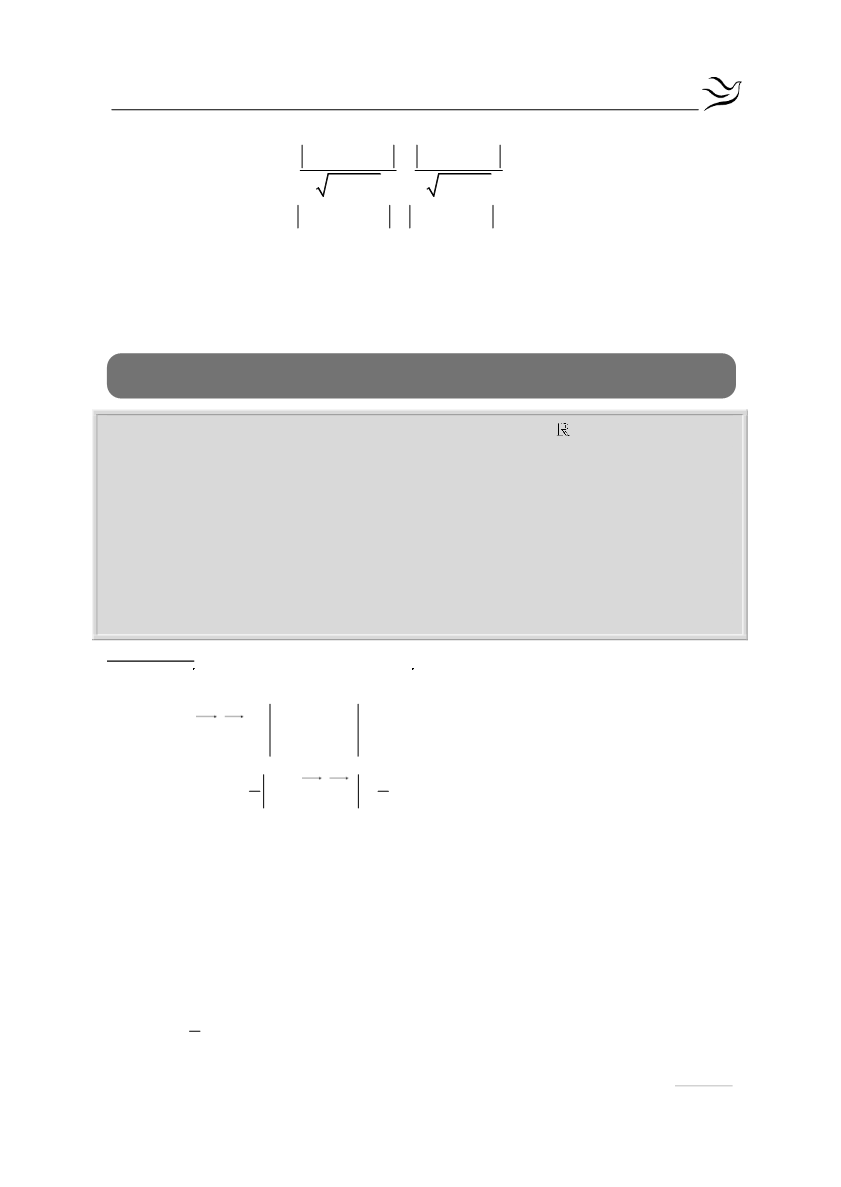
4x 3y 13 4x 3y 3
d Δ,ε d Δ,ε
4 3 4 3
4x 3y 13 4x 3y 3
4x 3y 13 4x 3y 3 αδύνατο ή 4x 3y 13 4x 3y 3 4x 3y 5 0
   
  
 
     
               
Επομένως η μεσοπαράλληλη των  
2 ε ,  
1 ε είναι η  ε : 4x 3y 5 0   και
οι συντεταγμένες των Α και Β επαληθεύουν την  ε .
Δίνονται τα σημεία       Α 1,2 , Β 3,4 , Γ 2λ 1,1 λ , λ    .
α. Να αποδείξετε ότι, για οποιαδήποτε τιμή του λ, τα Α, Β, Γ σχηματίζουν
τρίγωνο και το εμβαδόν του τριγώνου ΑΒΓ είναι σταθερό.
(Μονάδες 12)
β. Να αποδείξετε ότι η κορυφή Γ κινείται σε ευθεία παράλληλη στην ΑΒ.
(Μονάδες 6)
γ. Να βρείτε τις συντεταγμένες του Γ ώστε το τρίγωνο ΑΒΓ να είναι ορθογώνιο
με υποτείνουσα την ΒΓ.
(Μονάδες 7)
Απάντηση:
α. Είναι     ΑΒ 3 1,4 2 4,2 ,          ΑΓ 2λ 1 1,1 λ 2 2λ, 1 λ       
και   4 2
det ΑΒ,ΑΓ 4λ 4 4λ 4.
2λ 1 λ

    
 
Οπότε:     1 1
ΑΒΓ det ΑΒ,ΑΓ 4 2.
2 2
  
Άρα το εμβαδόν του ΑΒΓ είναι σταθερό.
β. Είναι:
Γ Γ Γ x 2λ 1 και y 1 λ λ 1 y       
οπότε  
Γ Γ Γ Γ Γ x 2λ 1 x 2 1 y 1 x 2y 3 0          .
Αφού οι συντεταγμένες του Γ επαληθεύουν την εξίσωση x 2y 3 0   , το Α
κινείται στην ευθεία  ε : x 2y 3 0   που έχει συντελεστή διεύθυνσης
ε
1
λ
2
  .
ΘΕΜΑ 4 - 22571