Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
96
ε)
Για δύο ενδεχόμενα Α και Β ενός δειγματικού χώρου Ω με
A B
Í
,
ισχύει ότι
( ) ( )
P A P B
>
.
(Μονάδες 10)
Απάντηση:
Α
1.
Έχουμε
(
) ( ) (
)
+ - = + - =
f x h f x x h x h
,
και για
¹
h 0
,
(
) ( )
+ -
= =
f x h f x h
1
h
h
.
Επομένως
,
(
) ( )
®
®
+ -
= =
h 0
h 0
f x h f x
lim
lim1 1
h
,
άρα
( )
f ' x 1
=
.
Σχολικό βιβλίο, Σελ.
28.
Α2.
Μια συνάρτηση
f
με πεδίο ορισμού το Α, θα λέμε ότι παρουσιάζει τοπικό
ελάχιστο στο
0
x
A
Î
,
όταν
0
f(x) f(x )
³
για κάθε
x
σε μια περιοχή του
0
x
.
Σχολικό βιβλίο, Σελ.
14.
Α3.
Διάμεσος (δ) ενός δείγματος ν παρατηρήσεων
,
οι οποίες έχουν διαταχθεί
σε αύξουσα σειρά ορίζεται ως η μεσαία παρατήρηση, όταν το ν είναι περιττός
αριθμός ή ο μέσος όρος (ημιάθροισμα) των δύο μεσαίων παρατηρήσεων
,
όταν
το ν είναι άρτιος αριθμός.
Σχολικό βιβλίο, Σελ.
87.
Α4.
α)
Λάθος
β)
Σωστό
γ)
Λάθος
δ)
Λάθος
ε)
Λάθος
Δίνεται ο δειγματικός χώρος
{
}
1 2 3 4
Ω ω ,ω ,ω ,ω
=
και τα ενδεχόμενα
{ }
1 4
Α ω ,ω
=
και
{ }
1 3
Β ω ,ω
=
Για τις πιθανότητες των απλών ενδεχομένων
{ }
1
ω
και
{ }
3
ω
του Ω ισχύει ότι:
·
2
1
3 2
x 1
1 x x 1 1
P(
ω )
lim
2
x x
®-
+ + -
= -
+
·
H
( )
3
P
ω
είναι ίση με το ρυθμό μεταβολής της
( )
f x
ως προς
x
, όταν
x 1
=
,
όπου
x
f(x)
lnx, x 0
3
=
>
.
Β1.
Να αποδείξετε ότι
1
1
P(
ω )
4
=
και
3
1
P(
ω )
3
=
.
(
Μονάδες 10
)
ΘΕΜΑ Β
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ
2013
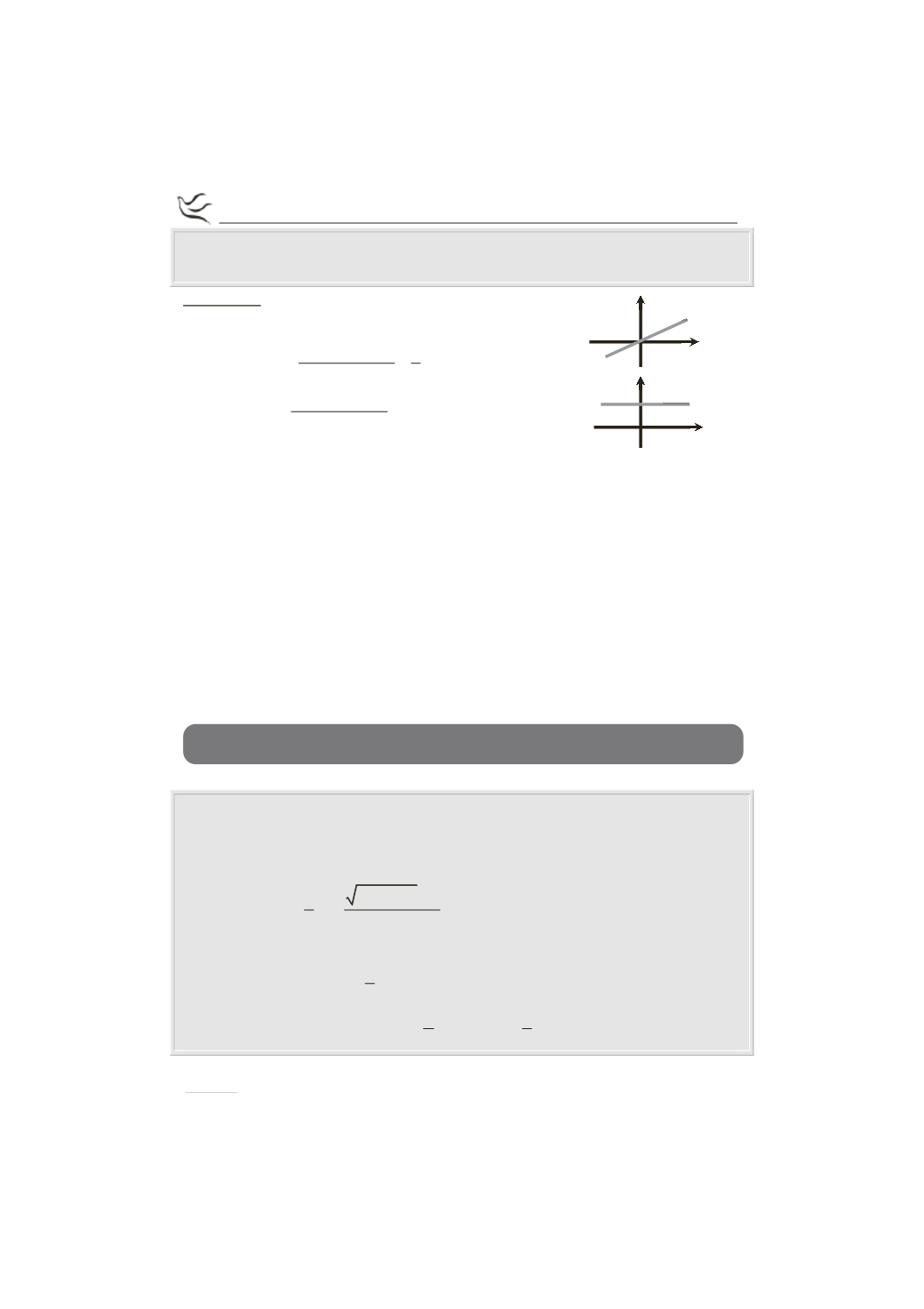
y=x
x
y
x
y
y=1









