93
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
·
( )
(
)
(
)
2
2
2
lnx 1
f ' x 0
0 lnx 1 0 lnx 1 x e
x
-
= Û-
= Û - = Û = Û =
·
( )
f ' x 0 x e
< Û ¹
και
x 0
>
.
Επειδή
( )
f ' x 0
<
για κάθε
( ) (
)
x 0,e e,
Î È +¥
, η
f
θα είναι γνησίως φθίνουσα
στο
(
)
0,
+¥
.
Ακολουθεί ο πίνακας μεταβολών της
f:
x
0
e
+¥
( )
f ' x
-
-
f
>
Δ2.
Έχουμε
:
·
x 0
>
·
1
2
2
ln x 0 1 ln x 1 0
+
³ Û + ³ >
·
Επομένως
,
2
1 ln x
0
x
+
>
ως πηλίκο
θετικών όρων. Δηλαδή
,
( )
f x 0
>
για κάθε
x 0
>
.
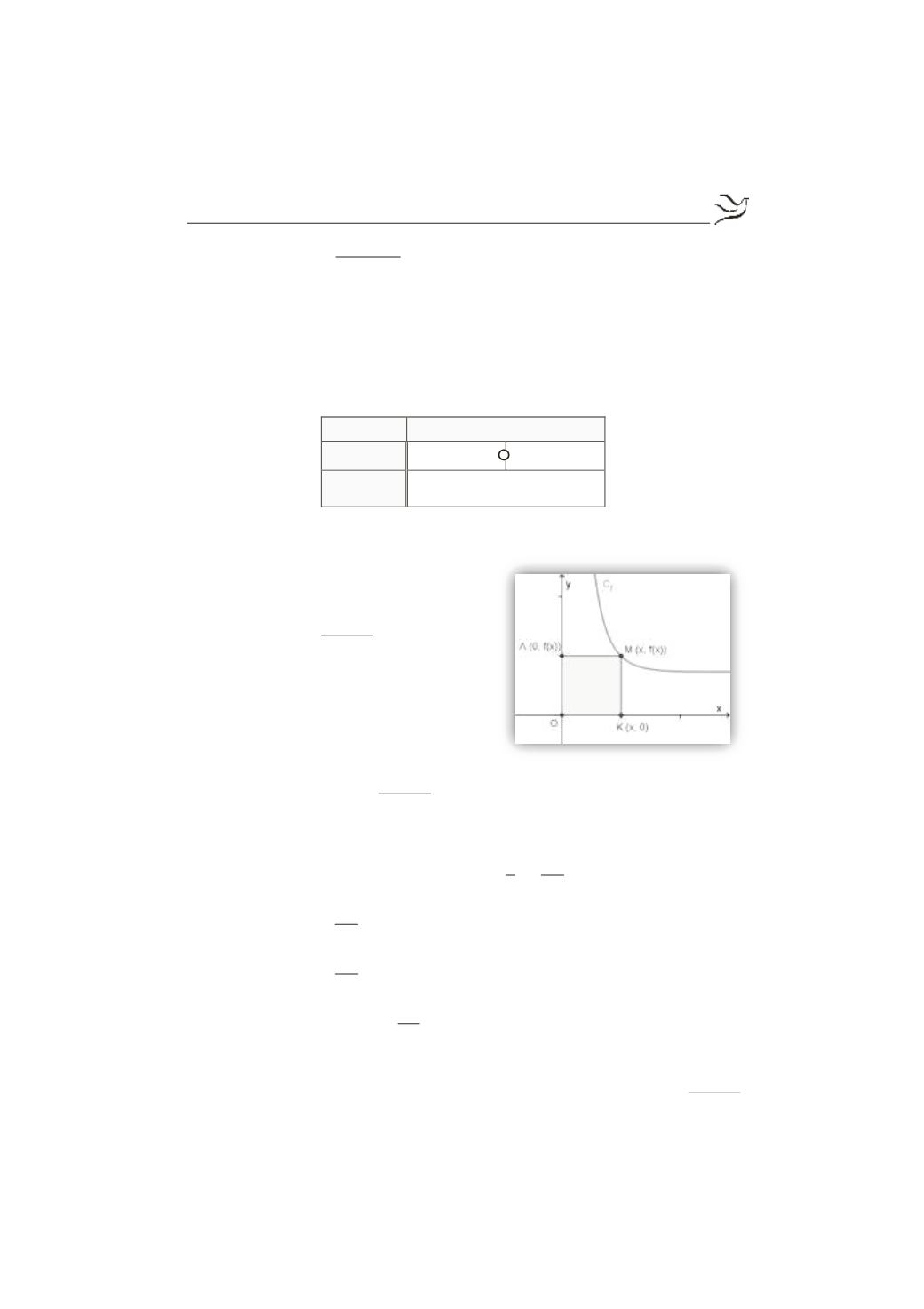
Τότε το ζητούμενο εμβαδόν του
ορθογωνίου θα ισούται με
:
( ) ( )
( )
2
2
1 ln x
E OK
ΟΛ x f x x
1 ln x
x
+
= ×
= ×
= ×
= +
.
Θεωρούμε τη συνάρτηση:
( )
2
E x 1 ln x
= +
με
x 0
>
.
Έχουμε:
·
( )
(
)
( )
2
1 lnx
E' x 1 ln x ' 2lnx lnx ' 2lnx 2
x x
= + = ×
= × =
, με
x 0
>
.
·
( )
lnx
E' x 0 2 0 lnx 0 x 1
x
= Û = Û = Û =
.
·
( )
lnx
2 0
x 0
lnx
E' x 0 2 0 lnx 0 lnx ln1 x 1
x
>
>
> Û > Û > Û > Û >
1
.
·
Ομοίως
( )
( )
lnx
2 0
x 0
lnx
E' x 0 2
0 lnx 0 lnx ln1 x 0,1
x
>
>
< Û ×
< Û < Û < Û Î
1
.









