Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
94
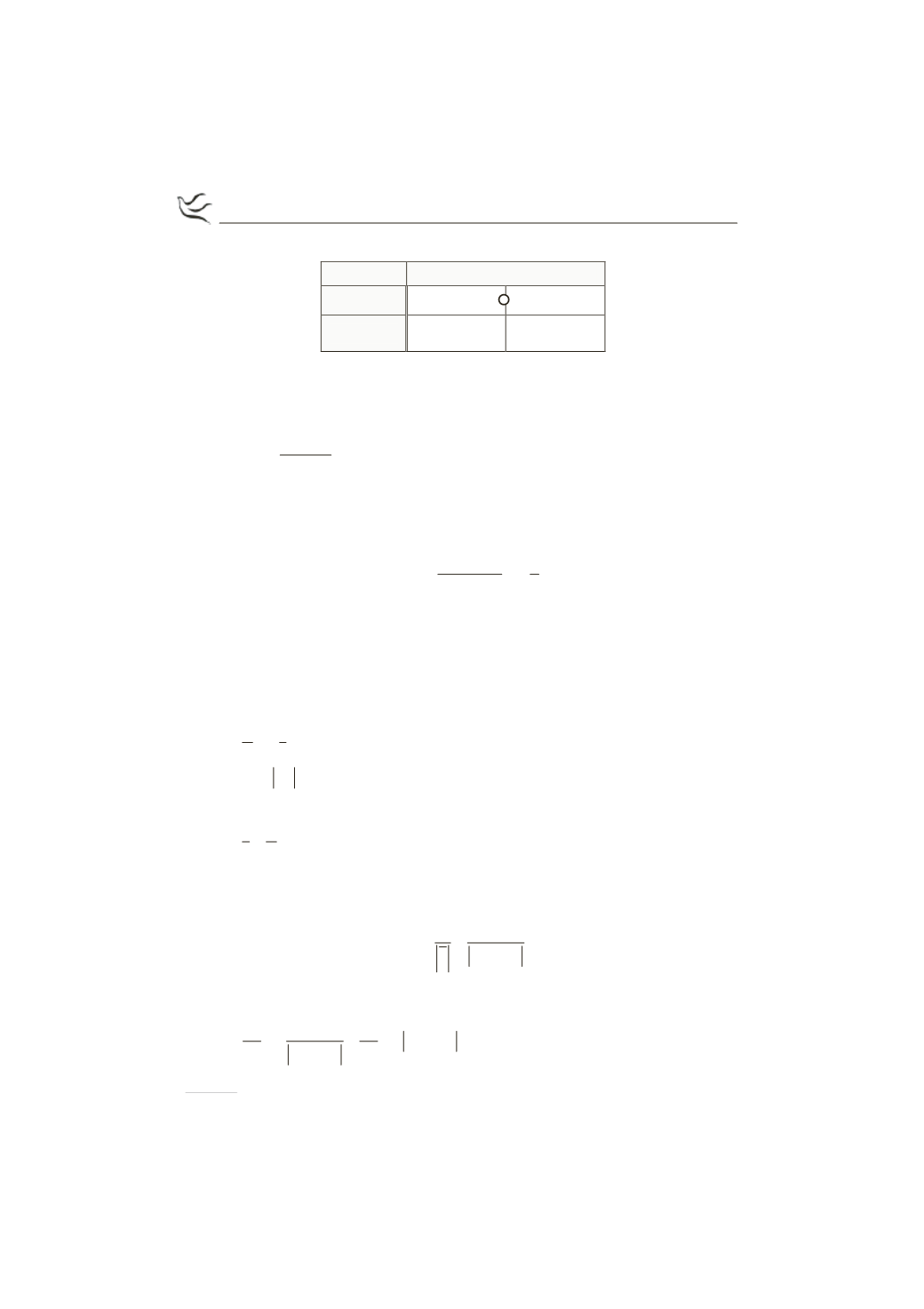
Ο πίνακας μεταβολών της συνάρτησης Ε είναι:
x
0
1
+¥
( )
E' x
-
+
E
>
1
Άρα η συνάρτηση
( )
2
E x 1 ln x
= +
,
x 0
>
παρουσιάζει ολικό ελάχιστο στο
x 1
=
,
ίσο με
( )
2
E 1 1 ln 1 1
= + =
. Τότε
,
όμως,
θα
είναι:
( )
OK x 1
= =
και
( ) ( )
2
1 ln 1
ΟΛ f 1
1
1
+
= =
=
, δηλαδή το ΟΚΜΛ είναι τετράγωνο πλευράς 1.
Δ3.
Εφόσον η ευθεία
ε: y λx β
= +
,
β 10
¹
,
είναι παράλληλη στην εφαπτομένη
της γραφικής παράστασης της
f
στο σημείο
( )
(
)
Σ 1, f 1
, θα ισχύει:
( ) (
)
2
2
ln1 1 1
λ f ' 1
1
1
1
-
= = -
= - = -
Τότε η ευθεία ε γίνεται
ε : y x β
= - +
με
β 10
¹
και τα 10 σημεία θα έχουν:
·
τετμημένες της μορφής
i
x
με
i 1,2,...,10
=
·
τεταγμένες της μορφής
i
i
y x
β
= - +
με
i 1,2,...,10
=
και
β 10
¹
Θεωρούμε το δείγμα
i
ω
που προκύπτει απ’ τις τετμημένες
i
x
ως εξής:
i
i
ω x
= -
,
με
i 1,2,...,10
=
. Τότε
,
σύμφωνα με την
εφαρμογή
3,
σελίδα
99
του σχολικού
βιβλίου
,
θα είναι:
·
ω x 10
= - = -
·
ω
x
s
1 s 2
= - × =
Ακόμη, θα είναι:
·
i
i
y
ω β
= +
με
i 1,2,...,10
=
και
β 10
¹
·
y
ω β 10 β
= + = - +
με
β 10
¹
·
y
ω
s s 2
= =
Τότε ο συντελεστή μεταβολής του δείγματος
i
y
θα ισούται με:
y
s
2
CV
10
β
y
= =
- +
Για να είναι ομοιογενές το δείγμα
i
y
, αρκεί:
10
β 20 β 10
1
2
1
CV
10
β 20
ή
ή
10 10
β 10
10
β 20
β 30
- + £ -
£ -
ì
ü ì
ü
ï
ï ï
ï
£ Û £ Û - + ³ Û
Û
í
ý í
ý
- +
ï
ï ï
ï
- + ³
³
î
þ î
þ
Ο
.E.









