Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
102
Β’ τρόπος:
Δημιουργούμε έναν
νέο πίνακα που περιέχει μόνο τις 3 πρώτες κλάσεις.
Προφανώς η συχνότητα
i
ν
κάθε κλάσης θα είναι ίση με
i
f
ν
×
, όπου
ν
το
μέγεθος του αρχικού δείγματος.
Kλάσεις
Κεντρικές
Τιμές
i
x
Σχετική
Συχνότητα
i
f
Συχνότητα
i
ν
i
i
x
ν
×
[
)
50,60
55
0,1
0,1
ν
×
5,5
ν
×
[
)
60,70
65
0,3
0,3
ν
×
19,5
ν
×
[
)
70,80
75
0,2
0,2
ν
×
15
ν
×
Τότε είναι:
3
i
i
i 1
1 2 3
1
5,5
ν 19,5ν 15ν
x '
x
ν
ν'
ν ν ν
40
ν
40 ν
0,1
ν 0,3ν 0,2ν
=
+ +
=
× =
=
+ +
=
=
+ +
å
0,6
ν
400 200
.
6 3
=
= =
Γ
4.
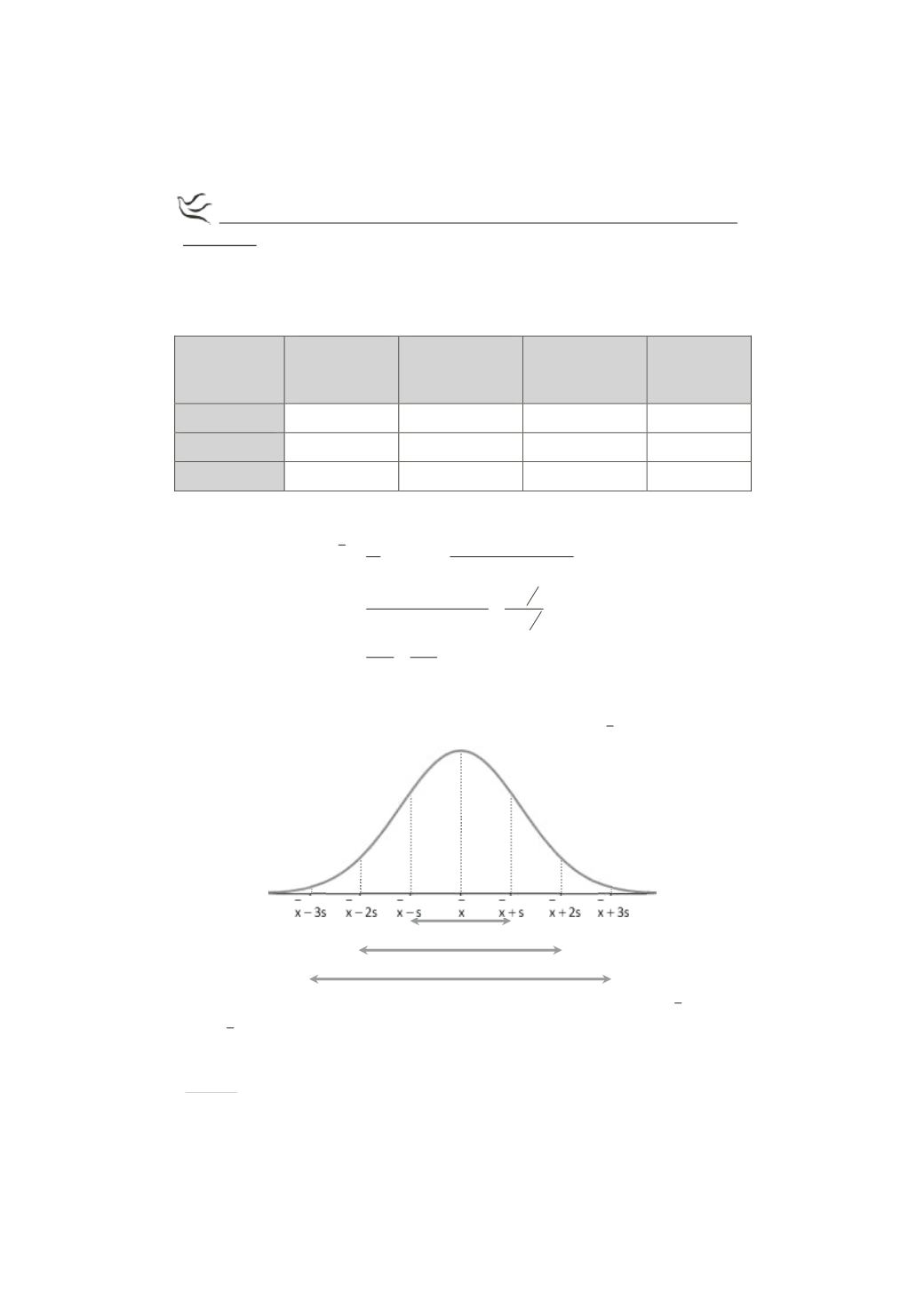
Αφού η κατανομή είναι κανονική και το 2,5% των παρατηρήσεων είναι
τουλάχιστον 74, θα είναι σύμφωνα με το παρακάτω σχήμα:
x 2s 74
+ =
.
Επίσης,
για το 16% των παρατηρήσεων που είναι το πολύ 68 θα είναι
x s 68
- =
,
όπου
x, s
η μέση τιμή και τυπική απόκλιση, αντίστοιχα, των κ παρατηρήσεων.
Άρα
,
θα έχουμε
:
0,15%
34%
34%
13,5%
13,5%
2,35%
2,35%
0,15%
68%
95%
99,7%









