Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
104
Α = {
t
Ω
Î
: η εφαπτομένη της γραφικής παράστασης της f
στο
σημείο
( )
(
)
t, f t
,
να σχηματίζει με τον άξονα
x
ʹ
x
οξεία γωνία
},
Β
= {
t
Ω
Î
:
( ) ( )
f t f ' t 1
> +
},
όπου
( )
f t tlnt 2
= +
.
Να βρεθούν οι πιθανότητες:
α)
να πραγματοποιηθεί το ενδεχόμενο Α
(
Μονάδες 3)
β)
να πραγματοποιηθούν συγχρόνως τα ενδεχόμενα Α και Β
(
Μονάδες 4)
Απάντηση:
Δ1.
Η συνάρτηση
f
είναι παραγωγίσιμη στο
(
)
0,
+¥
με:
( ) (
)
( )
f ' x xlnx
κ ' x' lnx x lnx ' lnx x
= + = ×
+ ×
= +
1
x
×
lnx 1
= +
.
·
Έστω
( )
ε : y λx β
= +
η εφαπτομένη της
f
C
στο σημείο
( )
(
)
M 1, f 1
.
·
Είναι:
( )
λ f ' 1 ln1 1 1
= = + =
.
·
Ισχύει:
( )
f 1 1 ln1
κ κ
= ×
+ =
, άρα το σημείο επαφής είναι το
( )
M 1,
κ
.
·
Αφού
( )
M
ε
Î
, θα είναι:
M M
y
λ x β κ 1 1 β β κ 1
= × + Û = × + Û = -
.
·
Επομένως
,
η εφαπτομένη γίνεται:
( )
ε : y x κ 1
= + -
.
·
Σημείο τομής της (ε) με τον άξονα
x
’
x
(
)
y 0
=
:
0 x
κ 1 x 1 κ
= + - Û = -
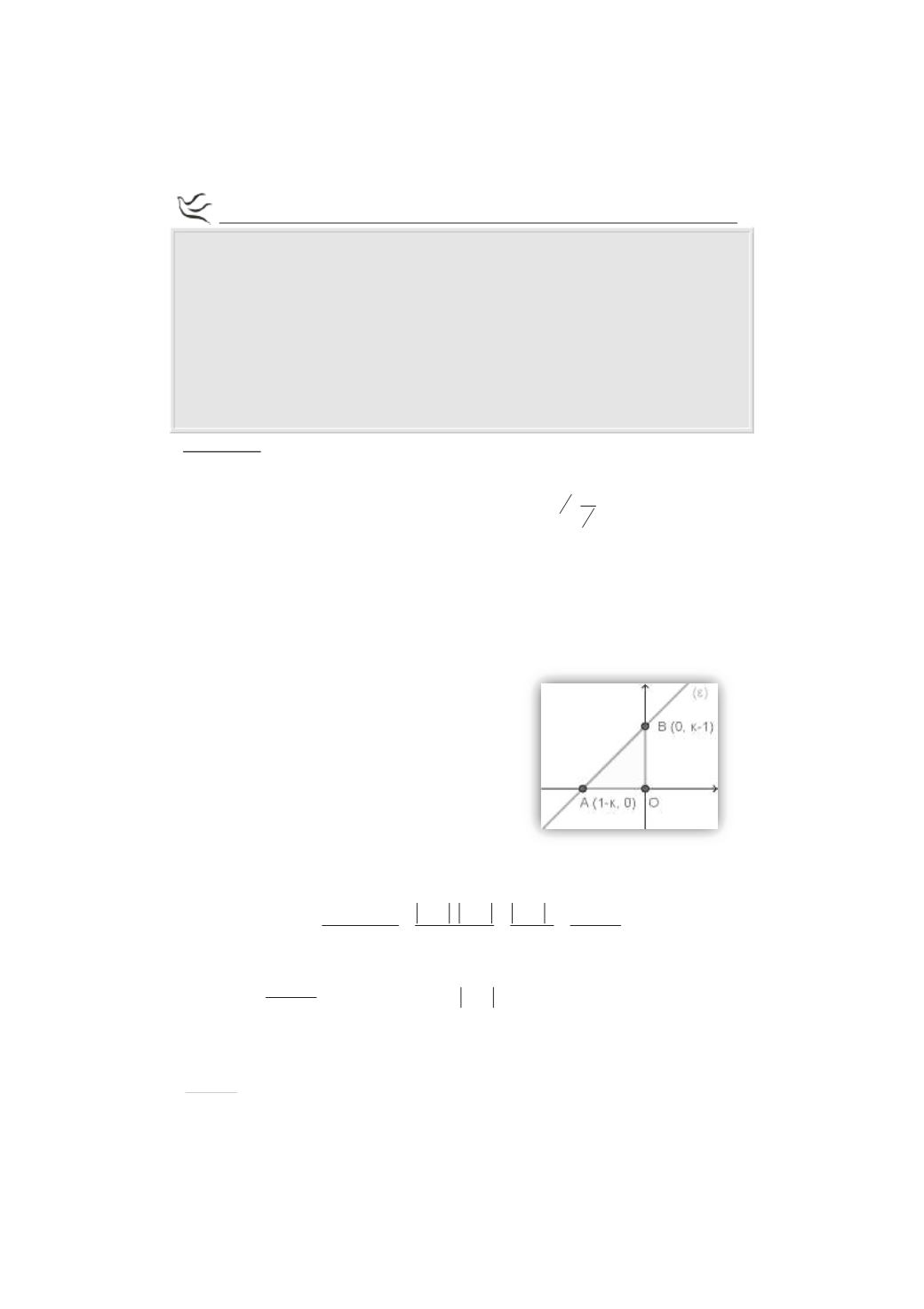
, άρα
το σημείο έχει τη μορφή
(
)
A 1
κ,0
-
.
·
Σημείο τομής της (ε) με τον άξονα
y
’
y
(
)
x 0
=
:
y 0
κ 1 y κ 1
= + - Û = -
, άρα
το σημείο έχει τη μορφή
(
)
B 0,
κ 1
-
.
Τότε το εμβαδόν του τριγώνου ΟΑΒ είναι:
( ) ( )
(
)
2
2
1
κ κ 1 κ 1
ΟΑ ΟΒ
κ 1
Ε
2
2
2
2
- × - -
×
-
=
=
=
=
.
Σύμφωνα με
την εκφώνηση θα είναι:
(
)
(
)
2
2
κ 1
E 2
2
κ 1 4 κ 1 2 2 κ 1 2 1 κ 3
2
-
< Û < Û - < Û - < Û- < - < Û- < <
Όμως, ο κ είναι ακέραιος με
κ 1
>
, επομένως θα είναι
κ 2
=
.









