Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
106
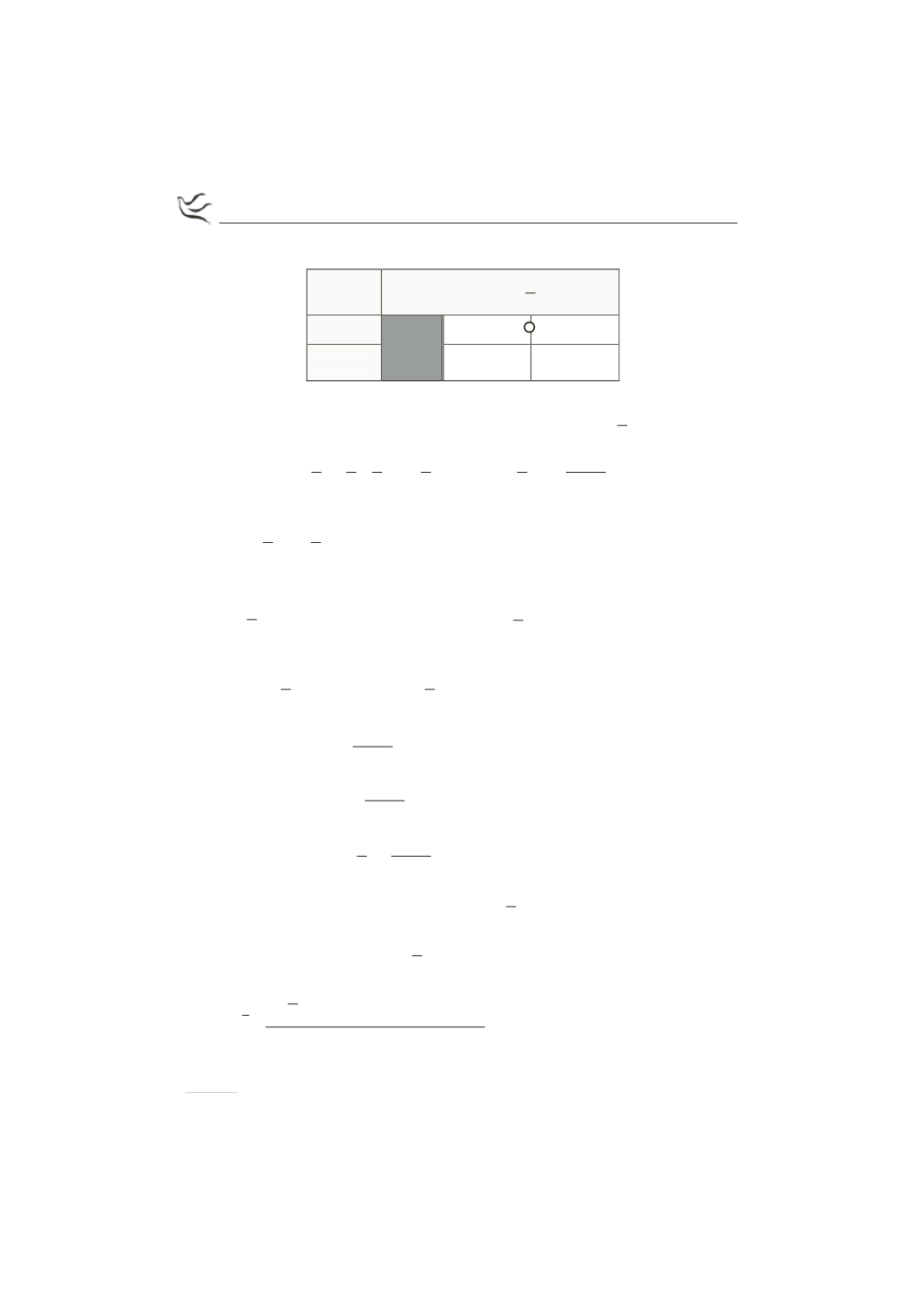
Συνεπώς ο πίνακας μεταβολών της συνάρτησης
f
είναι ο:
x
1
0
e
-¥
+¥
( )
f ' x
-
+
f
>
1
Επομένως η συνάρτηση
f
παρουσιάζει ολικό ελάχιστο στο
1
x
e
=
, το
1
1 1 1 1
1 2e 1
f
ln 2 lne 2
2
0
e e e e
e
e
-
-
æ ö = + =
+ = - + = >
ç ÷
è ø
Ισχύουν:
·
1
1 1
f '
ln 1 lne 1 1 1 0
e e
-
æ ö = + = + = - + =
ç ÷
è ø
·
( )
f e elne 2 e 2
=
+ = +
Οι τιμές
1
,
α, β, γ, e
e
ανήκουν στο διάστημα
1
,
e
é
ö +¥ ÷
êë
ø
, στο οποίο η συνάρτηση
f
είναι γνησίως αύξουσα, συνεπώς θα ισχύει:
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
f
1
1
α β γ e f
f α f β f γ f e
e
e
2e 1
f
α f β f γ f e
e
2e 1
0
f
α f β f γ f e
e
1 2e 1
f '
f
α f β f γ f e
e e
æ ö
< < < < Û < < < < Û
ç ÷
è ø
-
Û < < < < Û
-
Û < < < < < Û
-
æ ö
Û < < < < <
ç ÷
è ø
1
Τότε για τις τιμές
( )
f
α
,
( )
f
β
,
( )
f
γ
,
( )
f e
,
1
f '
e
æ ö
ç ÷
è ø
είναι:
·
( )
1
R max min f e f '
e 2 0 e 2
e
æ ö
= - = - = + - = +
ç ÷
è ø
·
( ) ( ) ( ) ( )
1
f '
f
α f β f γ f e
e
x
5
æ ö + + + +
ç ÷
è ø
=
. Όμως από την εκφώνηση ισχύει:
Ο
.E.









