75
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
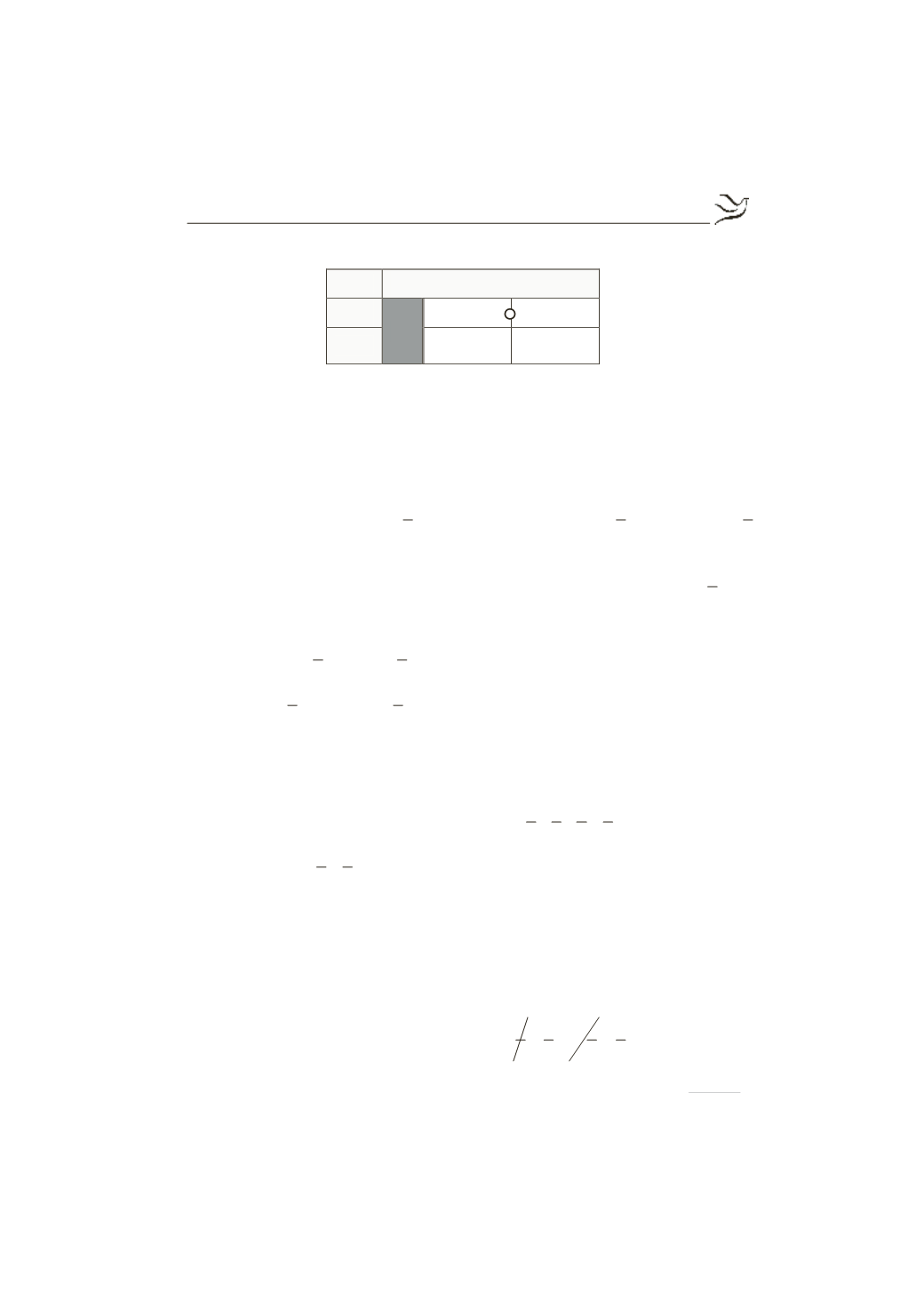
Ακολουθεί ο πίνακας μεταβολών της συνάρτησης
f:
x
( )
(
)
P A 1 P A
+
+¥
( )
f ' x
+
-
f
1
>
Επομένως η
f
είναι
:
·
Γνησίως αύξουσα στο
( )
( )
(
P A ,1 P A
+ ùû
·
Γνησίως φθίνουσα στο
( )
)
1 P A ,
é + +¥
ë
Η
f
παρουσιάζει ολικό μέγιστο στο
( )
x 1 P A
= +
, το
(
)
(
) (
)
2
2
1
1
1
f 1 P(A) ln 1 P(A) P(A)
1 P(A) P(A)
P(B) ln1 1 P(B) P(B)
2
2
2
+ = + - - + - + = - × + = -
Δ2.
Εφόσον η συνάρτηση παρουσιάζει ολικό μέγιστο στο σημείο
0
5
x
3
=
με
τιμή
( )
0
f x 0
=
, θα ισχύουν:
·
( )
( )
5
2
1 P A
P A
3
3
+ = Û =
·
( )
( )
1
1
P B 0 P B
2
2
- = Û =
Δ3.
Η ζητούμενη πιθανότητα είναι:
[
]
P (A B)' 1 P(A B)
Ç = - Ç
.
Όμως,
είναι:
P(A B) P(A) P(B) P(A B)
È = + -
Ç
,
άρα
2 1 5 1
P(A B) P(A) P(B) P(A B)
3 2 6 3
Ç = + - È = + - =
.
Άρα
,
1 2
P(A B)
΄ 1
3 3
Ç = - =
.
Δ4.
Η ζητούμενη πιθανότητα είναι η
(
) (
)
P A B B A
é - È - ù
ë
û
. Τα ενδεχόμενα
A B
-
και
B A
-
ξένα μεταξύ τους, οπότε από τον απλό προσθετικό νόμο θα έχουμε
ότι:
(
) (
)
(
) (
) ( ) (
) ( ) (
)
( )
( )
(
)
P A B B A P A B P B A P A P A B P B P A B
2
P A
P B 2P A B
3
é - È - ù = - + - = - Ç + - Ç =
ë
û
= + - Ç =
1 1
2
2 3
+ - ×
1
.
2
=
Ο
.M









