73
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
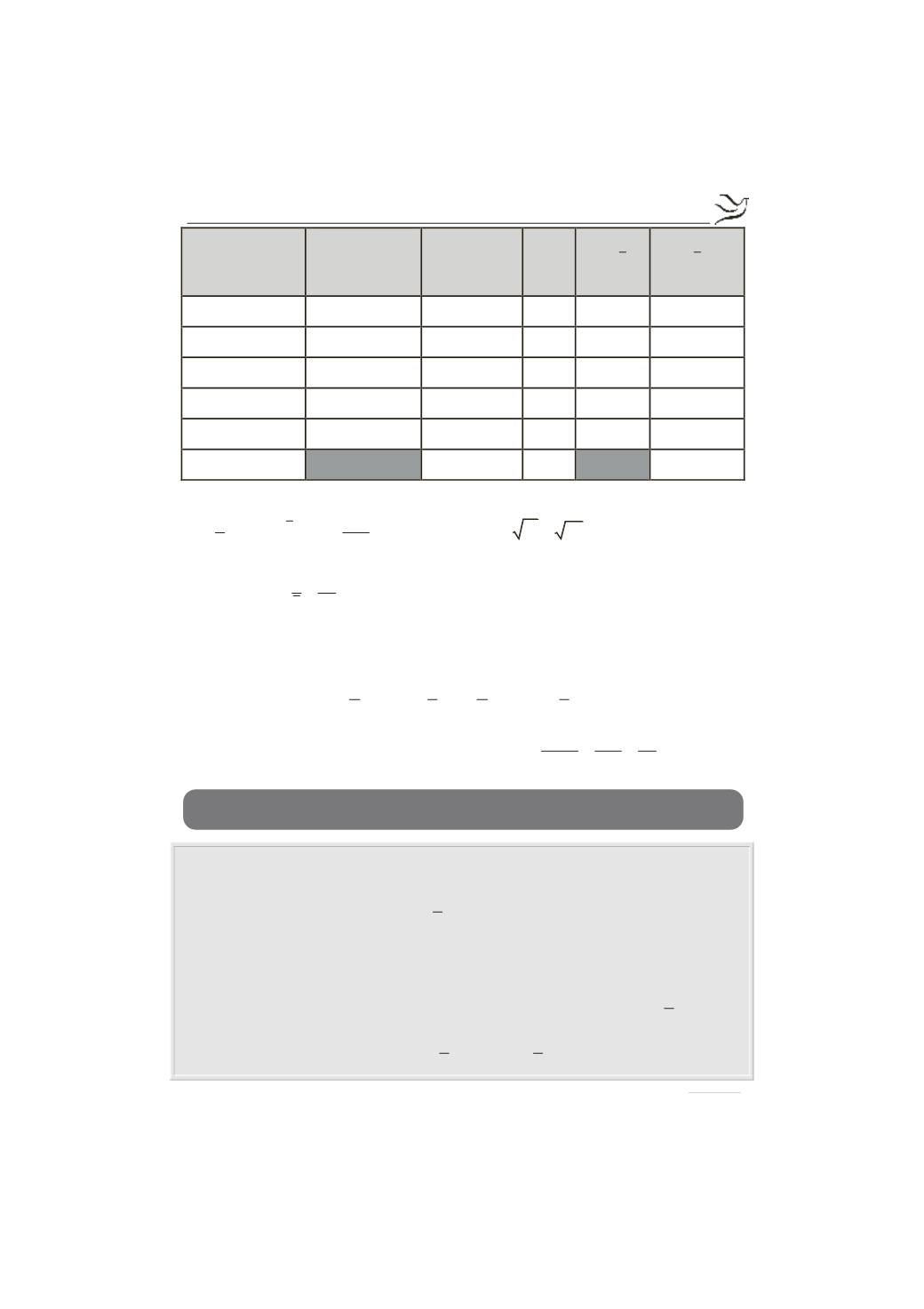
ΑΠΩΛΕΙΑ
ΒΑΡΟΥΣ
ΣΕ ΚΙΛΑ
ΚΕΝΤΡΟ
ΚΛΑΣΗΣ
i
x
ΣΥΧΝΟΤΗΤΑ
i
ν
i
i
x
ν
×
(
)
2
i
x
x
-
(
)
2
i
i
x x
ν
-
×
[
)
0,4
2
20
40
64
1280
[
)
4,8
6
40
240
16
640
[
)
8,12
10
45
450
0
0
[
)
12,16
14
30
420
16
480
[
)
16,20
18
25
450
64
1600
ΣΥΝΟΛΟ
160
1600
4000
Τότε είναι:
(
)
5
2
2
i
i
i 1
1
1
s
x x
ν
4000 25
ν
160
=
= ×
- × = ×
=
å
, άρα
2
s s
25 5
= = =
κιλά.
Γ3.
Είναι
:
s 5
CV
0,5
10 x
= = =
ή
50% 10%
>
.
Άρα
,
το δείγμα δεν είναι ομοιογενές.
Γ4.
Εφόσον τα δεδομένα έχουν ομαδοποιηθεί, θεωρούμε ότι οι παρατηρήσεις
είναι κατανεμημένες ομοιόμορφα μέσα στις κλάσεις, συνεπώς είναι:
( )
2 3
4
1
1 1
1
Ν Α ν ν
ν
40 45 30 70
4
2 4
2
= × + + × = × + + ×
=
Επιπλέον
,
είναι
( )
Ν Ω ν 160
= =
. Επομένως:
( ) ( )
( )
N A 70 7
P A
N
Ω 160 16
= = =
.
Έστω Α, Β δύο ενδεχόμενα ενός δειγματικού χώρου Ω με αντίστοιχες
πιθανότητες Ρ(Α), Ρ(Β) και η συνάρτηση
2
1
f(x) ln(x P(A)) (x P(A)) P(B), x P(A)
2
= - - - +
>
Δ1.
Να μελετήσετε τη συνάρτηση f ως προς τη μονοτονία και τα ακρότατα.
(
Μονάδες 13
)
Δ2.
Αν η συνάρτηση
f
παρουσιάζει ακρότατο στο σημείο
0
5
x
3
=
με τιμή
( )
0
f x 0
=
, να αποδείξετε ότι:
2
P(A)
3
=
και
1
P(B)
2
=
.
(
Μονάδες 2
)
ΘΕΜΑ Δ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 20
10









