67
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
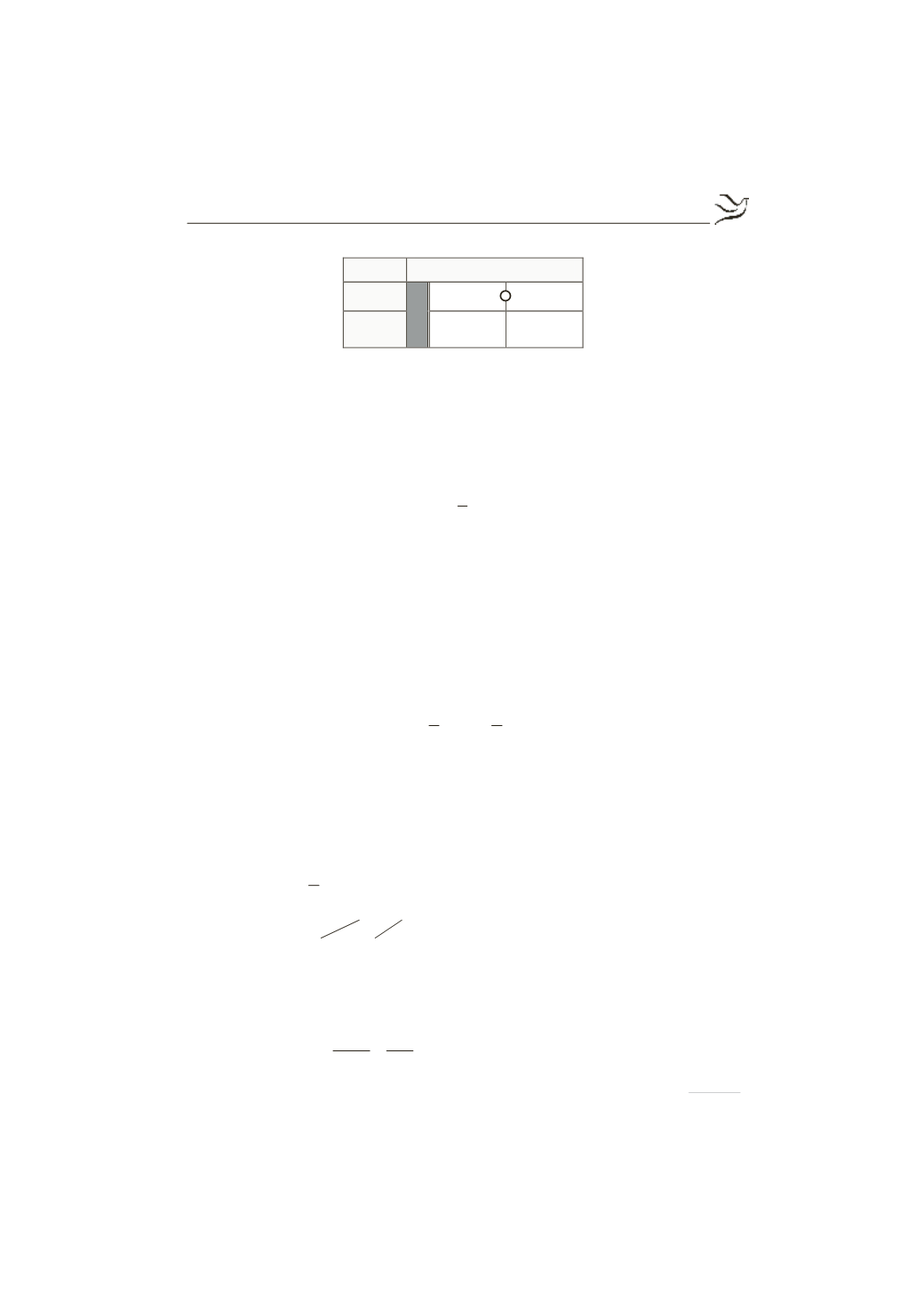
Ο πίνακας μεταβολών της
f
είναι:
x
0
2
+¥
( )
f ' x
+
-
f
1
>
Συνεπώς, η συνάρτηση
f
είναι:
·
Γνησίως αύξουσα στο
(
]
0,2
.
·
Γνησίως φθίνουσα στο
[
)
2,
+¥
.
β.
Από τον πίνακα μεταβολών συμπεραίνουμε ότι η συνάρτηση
f
παρουσιάζει
ολικό μέγιστο για
x 2
=
, το
( )
2
2
2
f 2 ln2
λ 6λ 2 ln2 λ 6λ 1
2
= - + - + = + - +
.
Β.α.
Οι τιμές 2, 3, 4, 5 και 8 ανήκουν στο διάστημα
[
)
2,
+¥
, στο οποίο η
συνάρτηση
f
είναι γνησίως φθίνουσα. Ισχύει:
[
)
( ) ( ) ( ) ( ) ( )
f 2,
2 3 4 5 8
f 2 f 3 f 4 f 5 f 8
+¥
< < < < Û > > > >
2
.
Επομένως:
·
Το εύρος είναι ίσο με:
( ) ( )
2
2
R f 2 f 8 (ln2
λ 6λ 1) (ln8 4 λ 6λ 2)
2
1
ln2 ln8 3 ln 3 ln 3.
8
4
= - = + - + - - + - + =
= - + = + = +
·
Η διάμεσος είναι ίση με τη μεσαία παρατήρηση, δηλαδή το
( )
f 4
,
αφού
το πλήθος των παρατηρήσεων είναι περιττός αριθμός. Δηλαδή:
( )
2
2
δ f 4 ln4 2 λ 6λ 2 ln4 λ 6λ
= = - + - + = + -
β.
Έχουμε διαδοχικά:
2
1
2
1
R
δ 2 ln 3 ln4 λ 6λ 2 ln4 3 ln4 λ 6λ 2 0
4
ln4
-
+ < - Û + + + - < - Û + + + - + < Û
Û -
ln4
+
2
2
λ 6λ 5 0 λ 6λ 5 0
+ - + < Û - + <
Το τριώνυμο έχει:
Δ 36 20 16
=
- =
και ρίζες:
λ 1
=
ή
λ 5
=
, επομένως η
ανίσωση
2
λ 6λ 5 0
- + <
αληθεύει για όσα
( )
λ 1,5
Î
, δηλαδή είναι:
{
} {
} { }
Α λ Ω|R δ 2
λ Ω|1 λ 5 2,3,4
= Î + < - = Î < < =
.
Τότε είναι:
( ) ( )
( )
N A 3
P A
3%
N
Ω 100
= = =
.
Ο
.M.









