Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
50
Εφόσον η μεταβλητή Χ ακολουθεί την κανονική κατανομή, προκύπτει το
ακόλουθο σχήμα:
Αφού τρεις παρατηρήσεις είναι μικρότερες ή ίσες του 8 είναι
:
0,15
ν 3 ν 2000
100
× = Û =
.
(i)
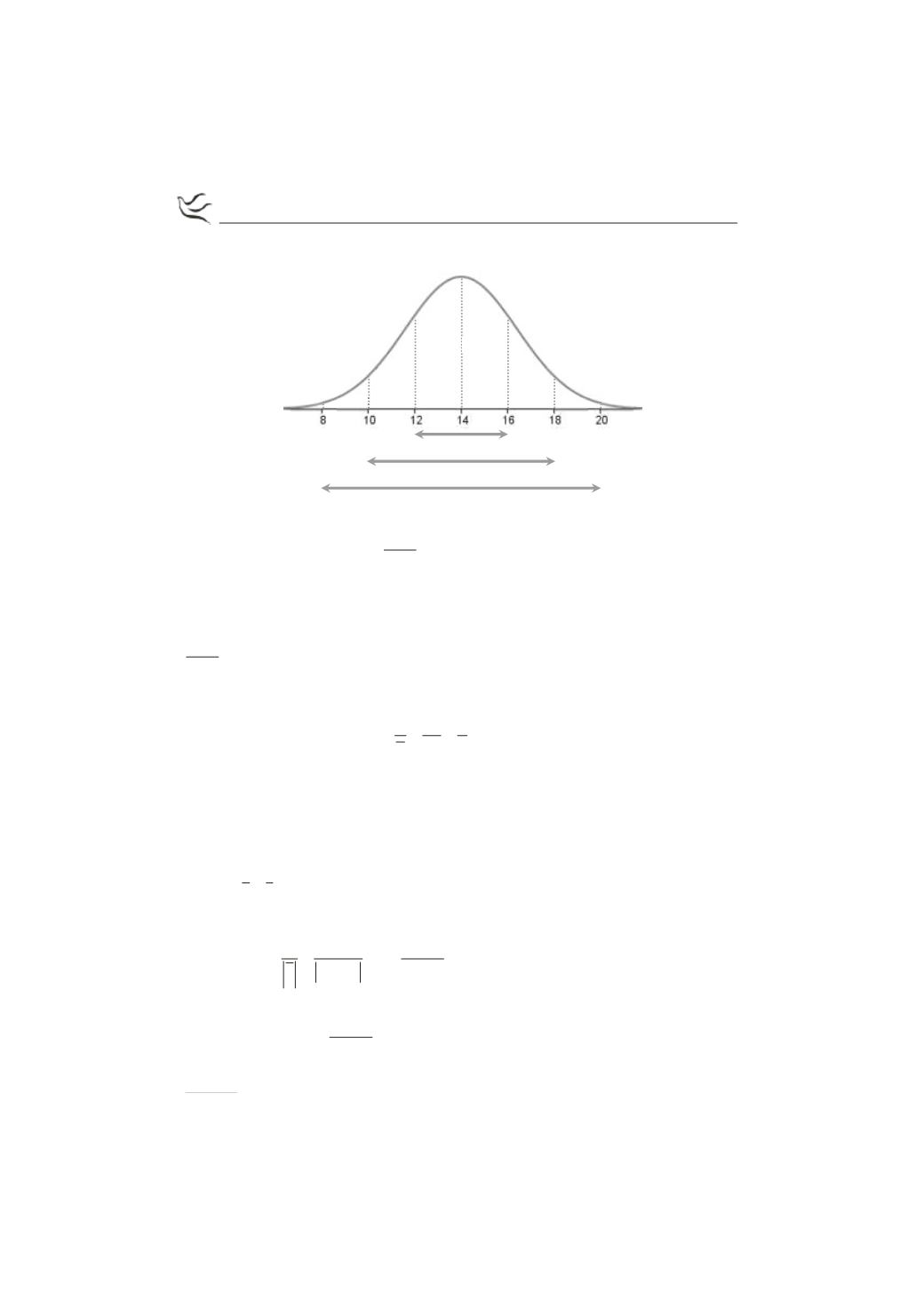
Στο διάστημα
(
)
10,16
όπως προκύπτει από το προηγούμενο διάγραμμα
βρίσκονται 81,5% του συνόλου
ν 2000
=
των παρατηρήσεων, δηλαδή
81,5
2000 1630
100
×
=
παρατηρήσεις.
(ii)
Ο συντελεστής μεταβολής του δείγματος είναι:
s 2 1
CV
0,14 0,10
x 14 7
= = = » >
.
Άρα το δείγμα δεν είναι ομοιογενές.
Θεωρούμε τη μεταβλητή
Y
με τιμές
i
i
y x
α
= +
, με
i
1,2,...,2000
=
, όπου
α 0
>
ο αριθμός που προσθέτουμε στις τιμές της μεταβλητής Χ, ώστε το νέο δείγμα
να είναι ομοιογενές. Σύμφωνα με την εφαρμογή 3, σελίδα
99 του σχολικού
βιβλίου θα ισχύει:
·
y x
α 14 α
= + = +
.
·
y
s s 2
= =
.
·
14
α 0
y
y
s
2
2
CV
14
α 14 α
y
+ >
= =
=
+
+
.
Για να είναι το νέο δείγμα ομοιογενές, αρκεί να ισχύει:
y
2
CV 10%
0,10 2 1,4 0,1
α 0,1α 0,6 α 6
14
α
£ Û £ Û £ + Û
³ Û ³
+
Έτσι η μικρότερη τιμή που μπορεί να πάρει η παράμετρος α είναι
α 6
=
.
0,15%
34%
34%
13,5%
13,5%
2,35%
2,35%
0,15%
68%
95%
99,7%









