223
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
( ) ( )
( )
3
2
f 1 1 3 1 4 2
- = - + × - - = -
Άρα, το ζητούμενο σημείο είναι το
(
)
Β 1, 2
- -
.
Β4.
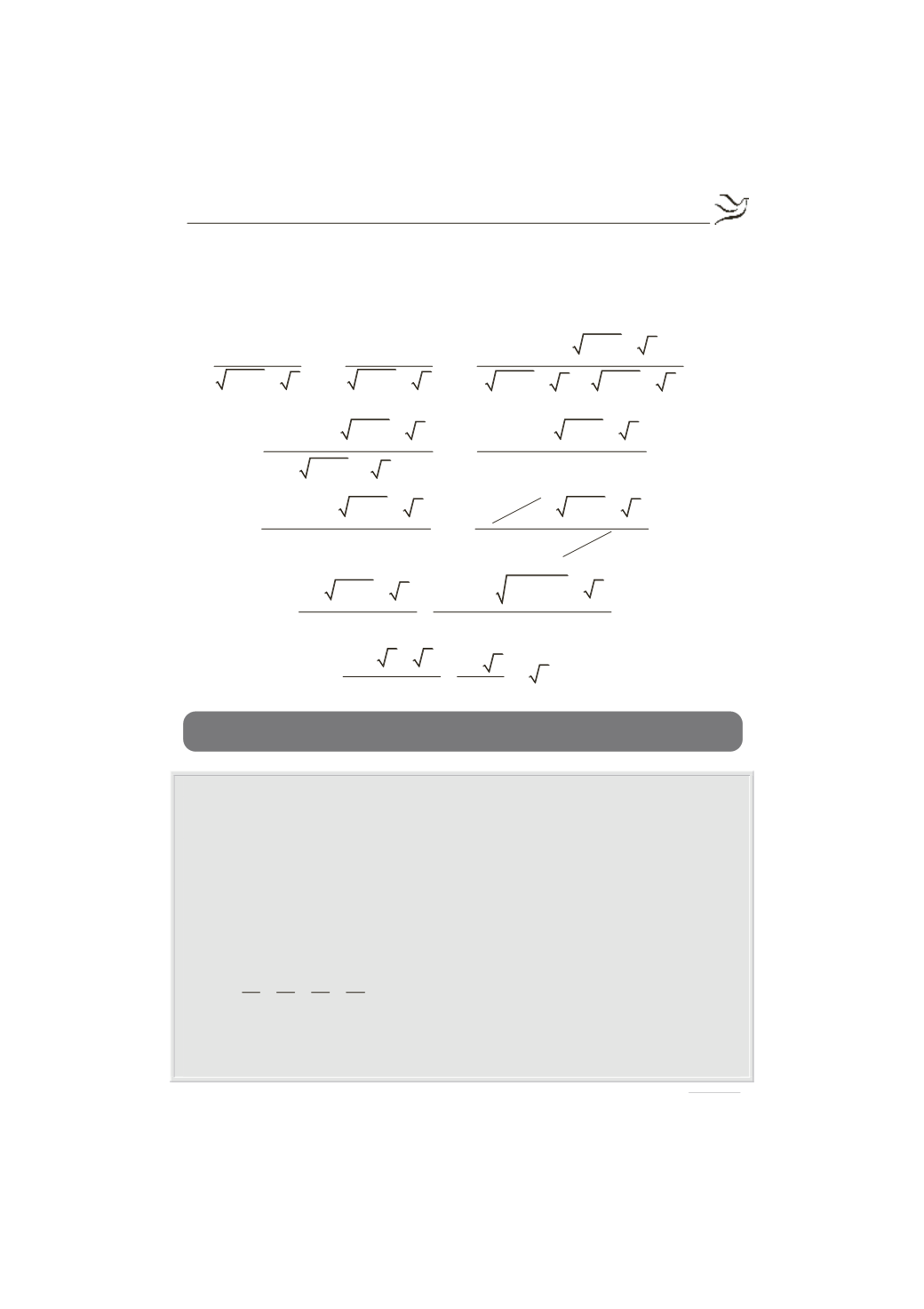
Έχουμε:
( )
(
)
(
)
(
) (
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
2
2
2
2
x 2
x 2
x 2
2
2
2
2
2
2
2
x 2
x 2
2
2
2
x 2
x 2
3x x 2 x 1 5
f x
3x 6x
lim
lim
lim
x 1 5
x 1 5
x 1 5 x 1 5
3x x 2 x 1 5
3x x 2 x 1 5
lim
lim
x 1 5
x 1 5
3x x 2 x 1 5
3x x 2
lim
lim
x 4
®-
®-
®-
®-
®-
®-
®-
+ ×
+ +
¢
+
=
=
=
+ -
+ -
+ - ×
+ +
+ ×
+ +
+ ×
+ +
=
=
=
+ -
+ -
+ ×
+ +
+
=
=
-
(
)
(
) (
)
2
x 1 5
x 2 x 2
×
+ +
- ×
+
(
)
( ) ( )
(
)
(
)
2
2
x 2
3 2
2 1 5
3x x 1 5
lim
x 2
2 2
6 5 5 6 2 5
3 5.
4
4
®-
=
× - ×
- + +
+ +
=
=
=
-
- -
- ×
+
×
=
=
=
-
Θεωρούμε ένα δείγμα ν συνδρομητών μιας εταιρείας κινητής τηλεφωνίας. Για
τον μήνα Μάιο, οι χρόνοι ομιλίας (σε ώρες) που έχουν χρεωθεί οι συνδρομητές
του δείγματος έχουν χωριστεί σε πέντε κλάσεις ίσου πλάτους. Θεωρούμε ότι οι
παρατηρήσεις κάθε κλάσης είναι ομοιόμορφα κατανεμημένες. Δίνεται ότι:
·
Η μικρότερη διάρκεια χρόνου ομιλίας που παρατηρήθηκε στο δείγμα
είναι μηδέν.
·
Το κέντρο της πέμπτης κλάσης είναι 18.
·
Στο κυκλικό διάγραμμα σχετικών συχνοτήτων, η γωνία του κυκλικού
τομέα που αντιστοιχεί στην πέμπτη κλάση ισούται με
o
36
.
·
3
1
2
4
N
N N
N
4 9 15 18
= = =
, όπου
1 2 3
N , N , N
και
4
N
είναι οι αθροιστικές
συχνότητες της 1
ης
, 2
ης
, 3
ης
και 4
ης
κλάσης αντίστοιχα.
Γ1.
Να αποδείξετε ότι το πλάτος
c
της κάθε κλάσης είναι 4.
(Μονάδες 4)
ΘΕΜΑ Γ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ
ΕΞΕΤΑΣΕΙΣ 2015









