Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
228
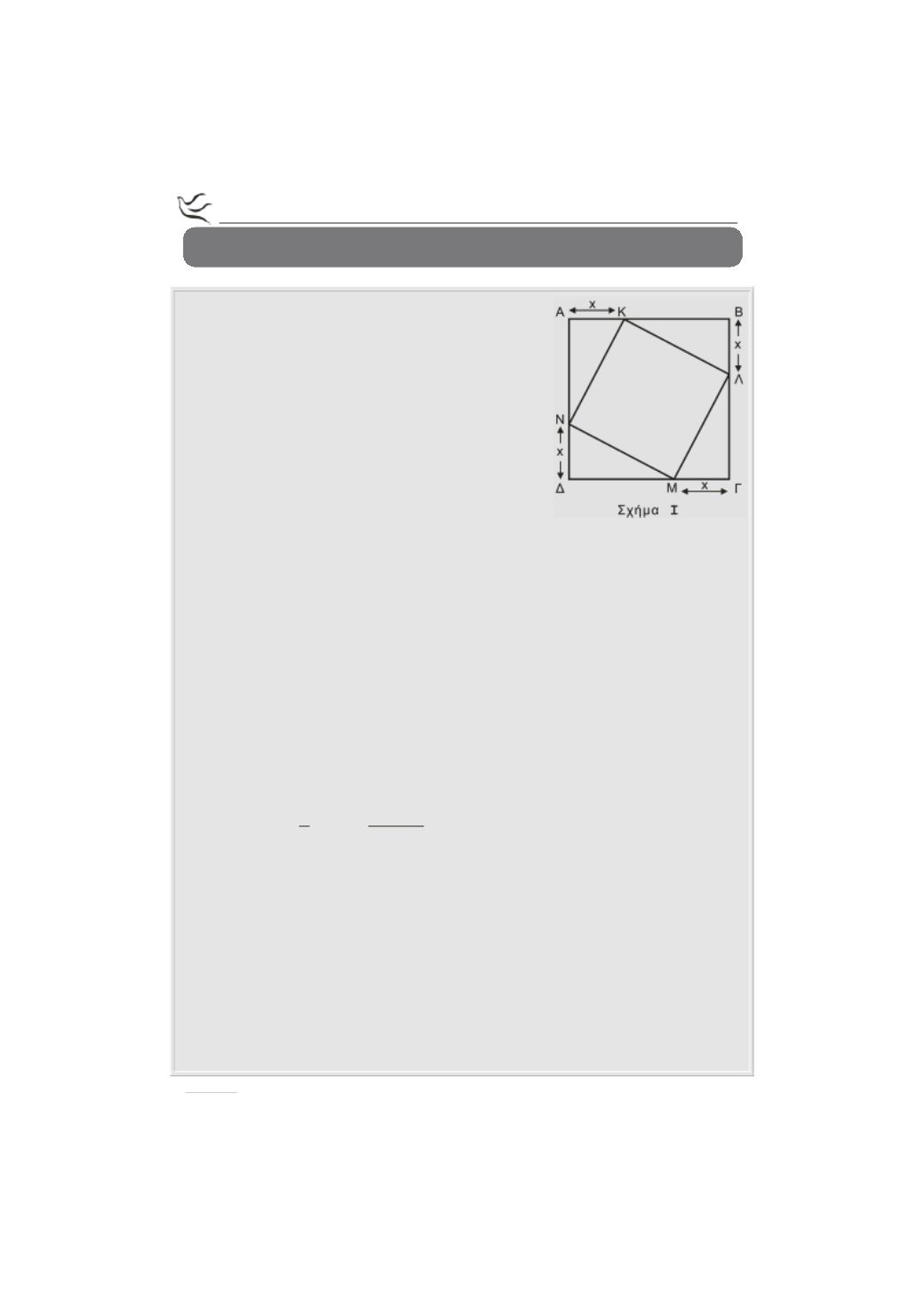
Δίνεται τετράγωνο πλευράς ΑΒΓΔ πλευράς 4.
Θεωρούμε τα εσωτερικά σημεία Κ, Λ, Μ και Ν των
πλευρών ΑΒ, ΒΓ, ΓΔ και ΔΑ αντίστοιχα, έτσι ώστε
ΑΚ ΒΛ ΓΜ ΔΝ x
=
= = =
,
όπως φαίνεται στο Σχήμα
I
.
Δ1.
Να αποδείξετε ότι το εμβαδόν του ΚΛΜΒ, ως
συνάρτηση του
x,
είναι:
( )
(
)
( )
2
E x 2 x 4x 8 , x 0,4
= - + Î
(Μονάδες 4)
Δ2.
Να βρείτε την τιμή του
x
για την οποία το
εμβαδόν
( )
E x
γίνεται ελάχιστο. (Μονάδες 4)
Δ3.
Θεωρούμε τις τιμές
( )
i
i
y E x
=
,
( )
i
x 0,4
Î
,
i 1,2,3,...,19
=
, έτσι ώστε:
·
Τα
i
x
,
i
1,2,3,...,19
=
είναι διαφορετικά μεταξύ τους.
·
Η μέση
τιμή των
i
x
,
i 1,2,3,...,19
=
και η διάμεσός τους είναι ίσες με 2.
·
Η μέση τιμή των
i
y
,
i 1,2,3,...,19
=
είναι ίση με 8,02.
α)
Να βρείτε τη μέση τιμή των
2
i
x
,
i 1,2,3,...,19
=
.
(Μονάδες 6)
β)
Να βρείτε την τυπική απόκλιση
x
s
των
i
x
,
i 1,2,3,...,19
=
και να εξετάσετε
αν το δείγμα τους είναι ομοιογενές.
(Μονάδες 5)
Δίνεται ότι
2
ν
i
ν
i 1
2
2
i
i 1
t
1
s
t
v
v
=
=
ì
ü
æ
ö
ï
ï
ç
÷
ï
ï
è
ø
=
- í
ý
ï
ï
ï
ï
î
þ
å
å
, όπου
i
t
,
i 1,2,...,
ν
=
είναι παρατηρήσεις
μιας μεταβλητής.
γ)
Επιλέγουμε τυχαία μία από τις τιμές
i
x
,
i 1,2,3,...,19
=
. Να βρείτε την
πιθανότητα των ενδεχομένων:
{
}
2
i
i
A x , i 1,2,3,...,19,
έτσι ώστε x 4
= =
³
( )
{
}
i
i
Β x , i 1,2,3,...,19, έτσι ώστε Ε x 8
= =
£
και
Γ: «Δεν πραγματοποιείται κανένα από τα ενδεχόμενα Α και Β».
(Μονάδες 6)
ΘΕΜΑ Δ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2015









