Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
222
Β2.
Είναι:
·
( )
(
)
3
2
2
f x x 3x 4 3x 6x, x
¢
¢
= + - =
+ Î
·
( )
(
)
2
f x 0 3x 6x 0 3x x 2 0 x 0
ή x 2
¢
= Û + = Û + = Û = = -
·
( )
(
) (
)
f x 0 x
, 2 0,
¢
> Û Î -¥ - È +¥
·
( )
(
)
f x 0 x 2,0
¢
< Û Î -
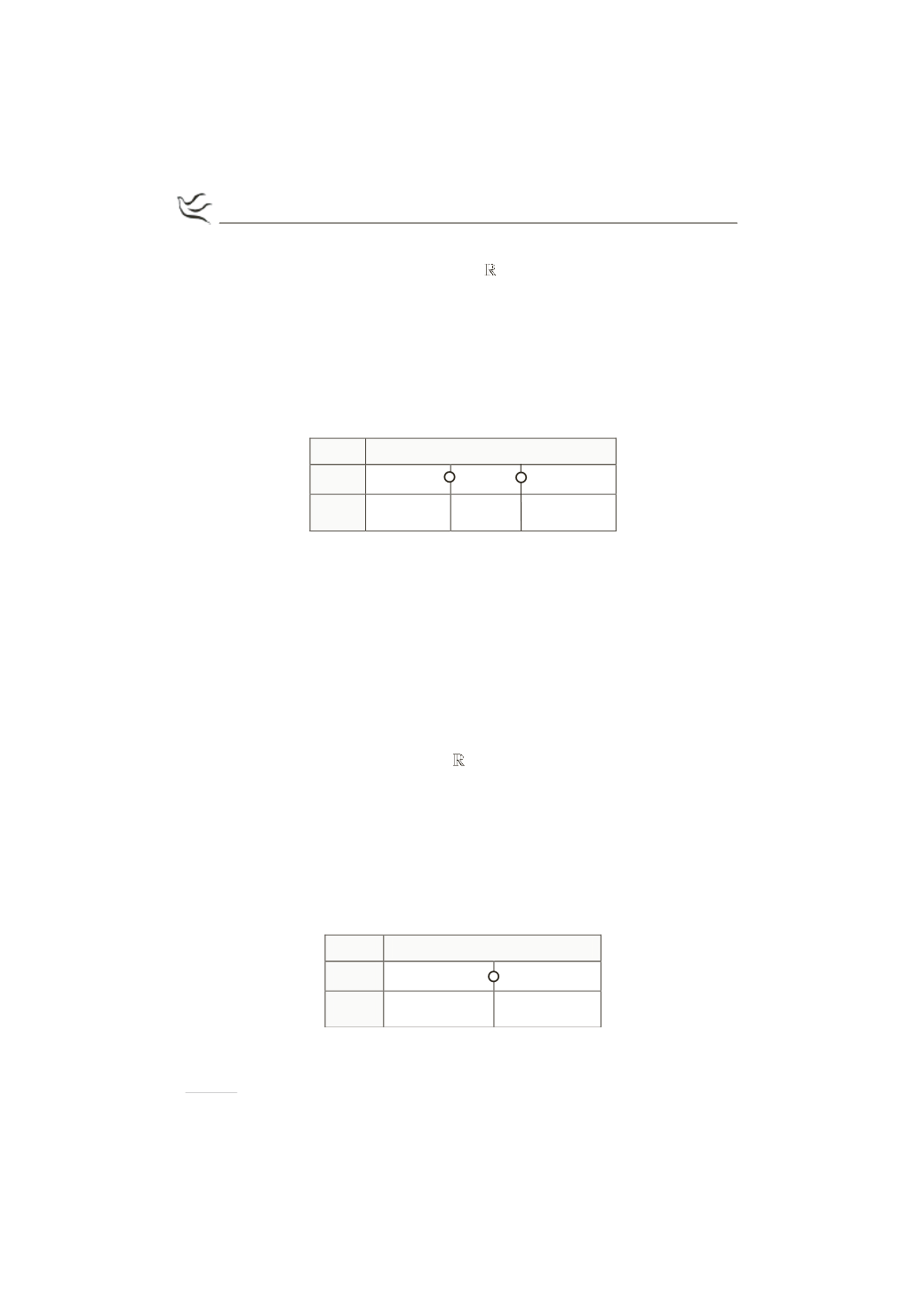
Ακολουθεί ο πίνακας μεταβολών της συνάρτησης
f:
Οπότε:
·
Η
f
είναι γνησίως αύξουσα στα διαστήματα
(
]
, 2
-¥ -
και
[
)
0,
+¥
·
Η
f
είναι γνησίως φθίνουσα στο διάστημα
[
]
2,0
-
·
Η
f
παρουσιάζει τοπικό μέγιστο στο
x 2
= -
το
( )
f 2
0
- =
·
Η
f
παρουσιάζει τοπικό ελάχιστο στο
x 0
=
το
( )
3
2
f 0 0 3 0 4 4
= + × - = -
.
Β3.
Αναζητούμε τα σημεία στα οποία η
( )
f x
¢
ελαχιστοποιείται. Είναι:
·
( )
(
)
2
f x 3x 6x 6x 6, x
¢
¢¢
= + = + Î
·
( )
f x 0 6x 6 0 x 1
¢¢
= Û + = Û = -
·
( )
f x 0 6x 6 0 6x 6 x 1
¢¢
> Û + > Û > - Û > -
·
( )
f x 0 6x 6 x 1
¢¢
< Û < - Û < -
Ακολουθεί ο πίνακας μεταβολών της συνάρτησης
f
¢
:
Συνεπώς, η
f
¢
παρουσιάζει ολικό ελάχιστο για
x 1
=-
. Επίσης,
x
-¥
2
-
0
+¥
( )
¢
f x
+
-
+
f
1
> 1
x
-¥
-
1
+¥
( )
f x
¢¢
-
+
f
¢
>
1
T.M.
T.E.
O.
Ε
.









