Μαθηματικά Γ' Λυκείου (Γενικής Παιδείας)

218 / 234

217
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Δίνεται ευθύγραμμο τμήμα ΑΒ με μήκος 100 m.
Θεωρούμε εσωτερικό σημείο Γ του ΑΒ τέτοιο,
ώστε το μήκος του τμήματος ΑΓ να είναι x m.
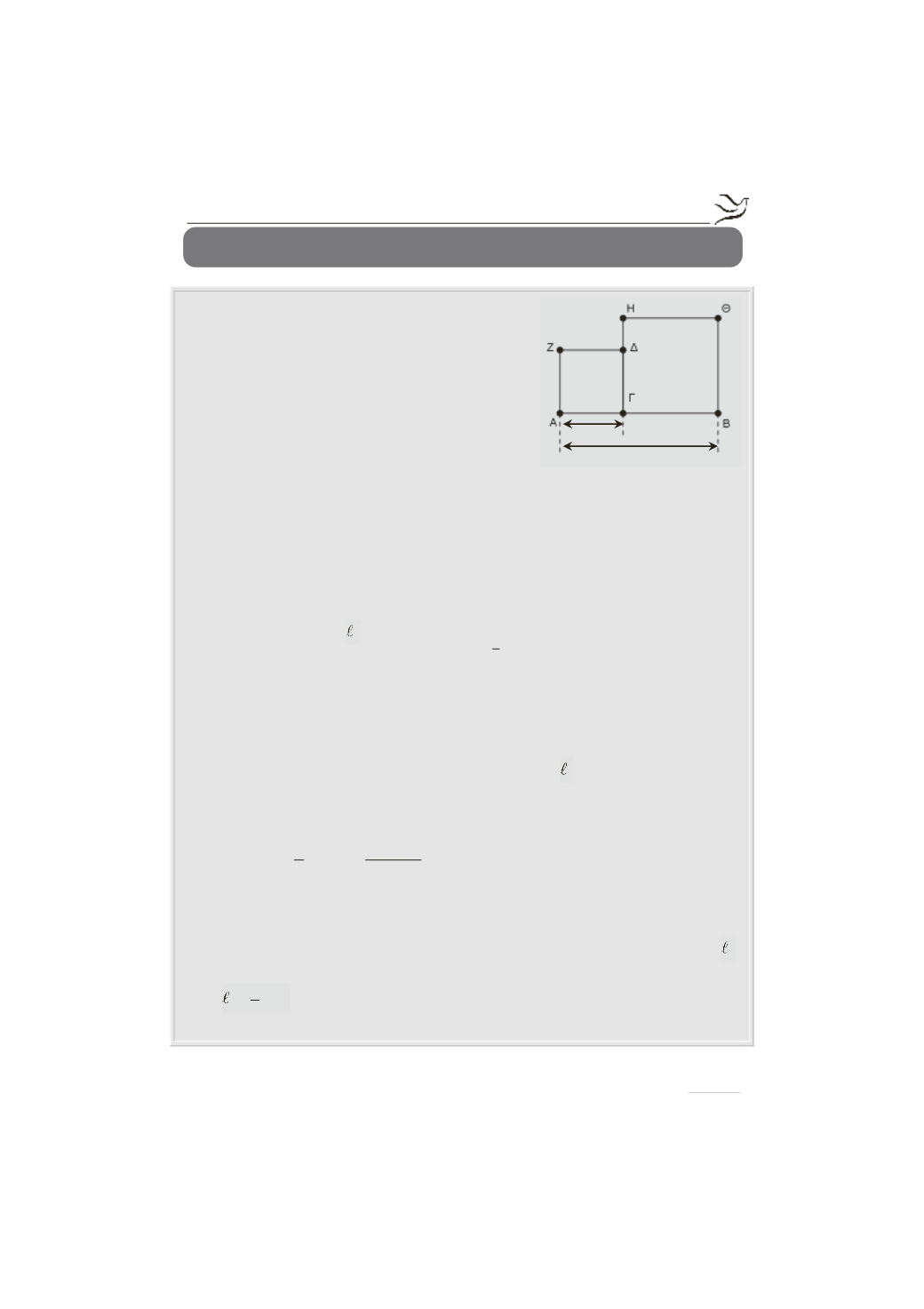
Δ1. Κατασκευάζουμε τα τετράγωνα ΑΓΔΖ και
ΓΒΘΗ, όπως φαίνεται στο διπλανό σχήμα.
i) Να αποδείξετε ότι το άθροισμα
των εμβαδών των δύο τετραγώνων, ως
συνάρτηση του x, είναι
( ) 2
E x 2x 200x 10000= - + , ( )
x 0,100Î (Μονάδες 3)
ii) Να βρείτε για ποια τιμή του x το εμβαδόν ( )
E x γίνεται ελάχιστο.
(Μονάδες 5)
Στη συνέχεια, για x 50= , χωρίζουμε το ευθύγραμμο τμήμα ΑΓ σε ν διαδοχικά
ευθύγραμμα τμήματα i , i 1,2,..., ν = με αντίστοιχα μήκη i x , i 1,2,..., ν = . Αν η
μέση τιμή των μηκών i x , i 1,2,..., ν = είναι x 2= και η τυπική απόκλιση είναι
s 0,2= τότε:
Δ2. Να δείξετε ότι ν 25= . (Μονάδες 5)
Δ3. Να βρείτε τη μέση τιμή των εμβαδών των τετραγώνων που
κατασκευάζονται με πλευρές τα διαδοχικά τμήματα i με αντίστοιχα μήκη i x ,
όπου i 1,2,...,25= .
Δίνεται ότι
2
ν
i
ν
i 1
2 2
i
i 1
t
1
s t
ν ν
=
=
ì ü
æ ö
ï ï
ç ÷
ï ï è ø
= - í ý
ï ï
ï ï
î þ
å
å . (Μονάδες 6)
Δ4. Επιλέγουμε τυχαία ένα από τα διαδοχικά ευθύγραμμα τμήματα i ,
i 1,2,...,25= . Να βρείτε την πιθανότητα του ενδεχομένου
Λ = { i , i 1,2,...,25= τέτοιο, ώστε ο δείκτης i να είναι πολλαπλάσιο του 3 ή
πολλαπλάσιο του }
4 . (Μονάδες 6)
ΘΕΜΑ Δ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2014
x
m 100
m