Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
226
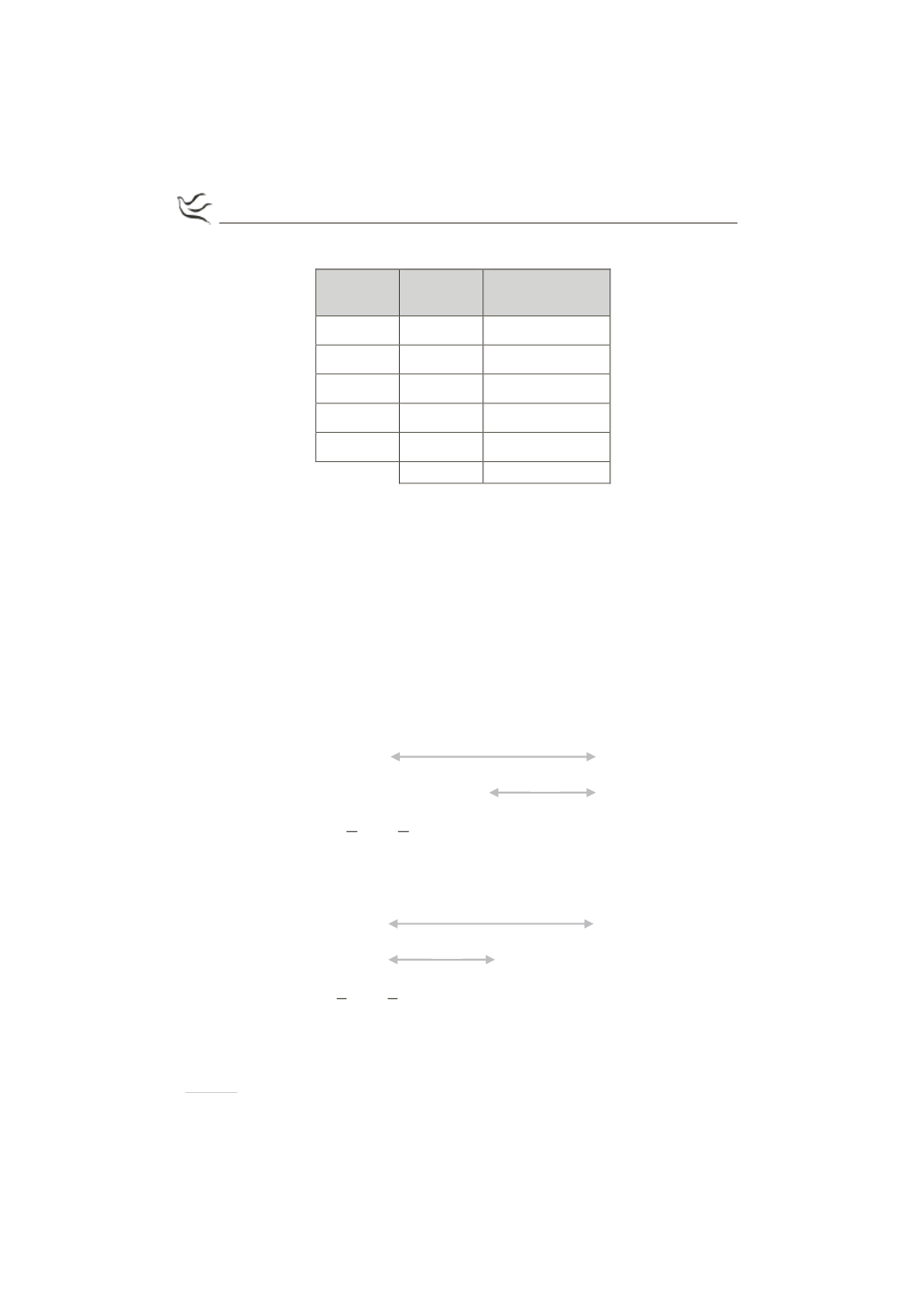
Ο πίνακας έχει ως εξής:
Κλάσεις
(σε ώρες)
Κεντρικές
τιμές
i
x
Σχετικές
συχνότητες
i
f %
[
)
0, 4
2
20
[
)
4, 8
6
25
[
)
8, 12
10
30
[
)
12, 16
14
15
[
)
16, 20
18
10
Σύνολο
100
Γ3.
Οι παρατηρήσεις, των οποίων το ποσοστό αναζητούμε, ανήκουν στο
διάστημα
[
)
3,10
. Εφόσον σε κάθε κλάση οι παρατηρήσεις κατανέμονται
ομοιόμορφα, το ζητούμενο ποσοστό θα είναι:
1
2
3
p f % f % f %
¢
¢
= + +
Όπου
1
f %
¢
το
ποσοστό των παρατηρήσεων που ανήκουν στο διάστημα
[
)
3,4
και
3
f %
¢
το ποσοστό των παρατηρήσεων που ανήκουν στο διάστημα
[
)
8,10
.
·
Για το
1
f %
¢
:
Δηλαδή,
1
1
1 1
f % f % 20 5
4 4
¢ = = =
·
Για το
3
f %
¢
:
Οπότε,
3
3
1 1
f % f % 30 15
2 2
¢ =
= =
Το ζητούμενο ποσοστό τότε είναι:
1
2
3
p f % f % f % 5 25 15 45
¢
¢
= + + = + + =
0
4
f
1
%
3
4
f
1
’
%
8
12
f
3
%
8
10
f
3
’
%









