17
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
λιγότερο από 10 λεπτά.
Υποθέτουμε ότι η κατανομή του χρόνου της διαδρομής είναι κατά προσέγγιση
κανονική.
Α.
Να βρείτε το μέσο χρόνο διαδρομής των μαθητών και την τυπική απόκλιση
του χρόνου διαδρομής τους.
(
Μονάδες 6
)
Β.
Να εξετάσετε, αν το δείγμα είναι ομοιογενές.
(
Μονάδες
6)
Γ.
Αν οι μαθητές της πόλης είναι 4.000, πόσοι μαθητές θα κάνουν χρόνο
διαδρομής από 14 έως 16 λεπτά.
(
Μονάδες 6
)
Δ.
Μια μέρα, λόγω έργων στον κεντρικό δρόμο της πόλης, κάθε μαθητής
καθυστέρησε 5 λεπτά. Να βρείτε πόσο μεταβάλλεται ο συντελεστής μεταβολής
(CV).
(
Μονάδες 7
)
Απάντηση:
Α.
Η κατανομή είναι περίπου
κανονική, άρα ισχύει:
δ x
=
. Εφόσον το 50% των
μαθητών χρειάζεται περισσότερο από 12 λεπτά, προκύπτει ότι
δ 12
=
, άρα
x 12
=
.
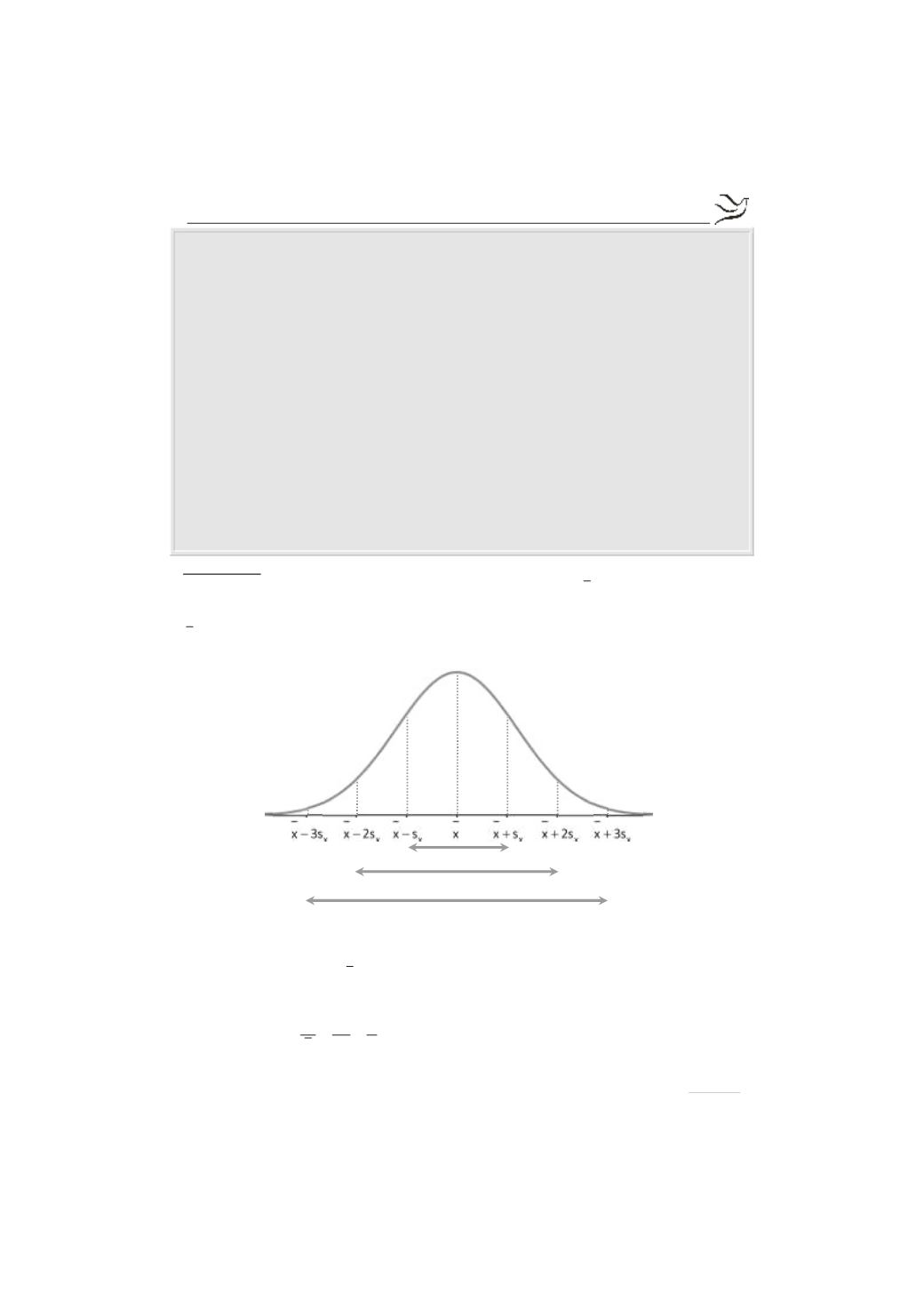
Ακόμη από το διάγραμμα της κανονικής κατανομής και από το γεγονός ότι το
16% των μαθητών έκαναν χρόνο λιγότερο από 10 λεπτά συμπεραίνουμε ότι:
x
x
x
x s 10 12 s 10 s 2
- = Û - = Û =
.
Β.
Είναι:
x
x
s 2 1
CV
0,166
12 6
x
= = = »
ή
16,6% 10%
>
, άρα το δείγμα δεν είναι
ομοιογενές.
0,15%
34%
34%
13,5%
13,5%
2,35%
2,35%
0,15%
95%
99,7%
68%









