Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
176
[
)
16,18
17
6
0,1
10
[
)
18,20
19
6
0,1
10
Σύνολο
60
1
100
Β2.
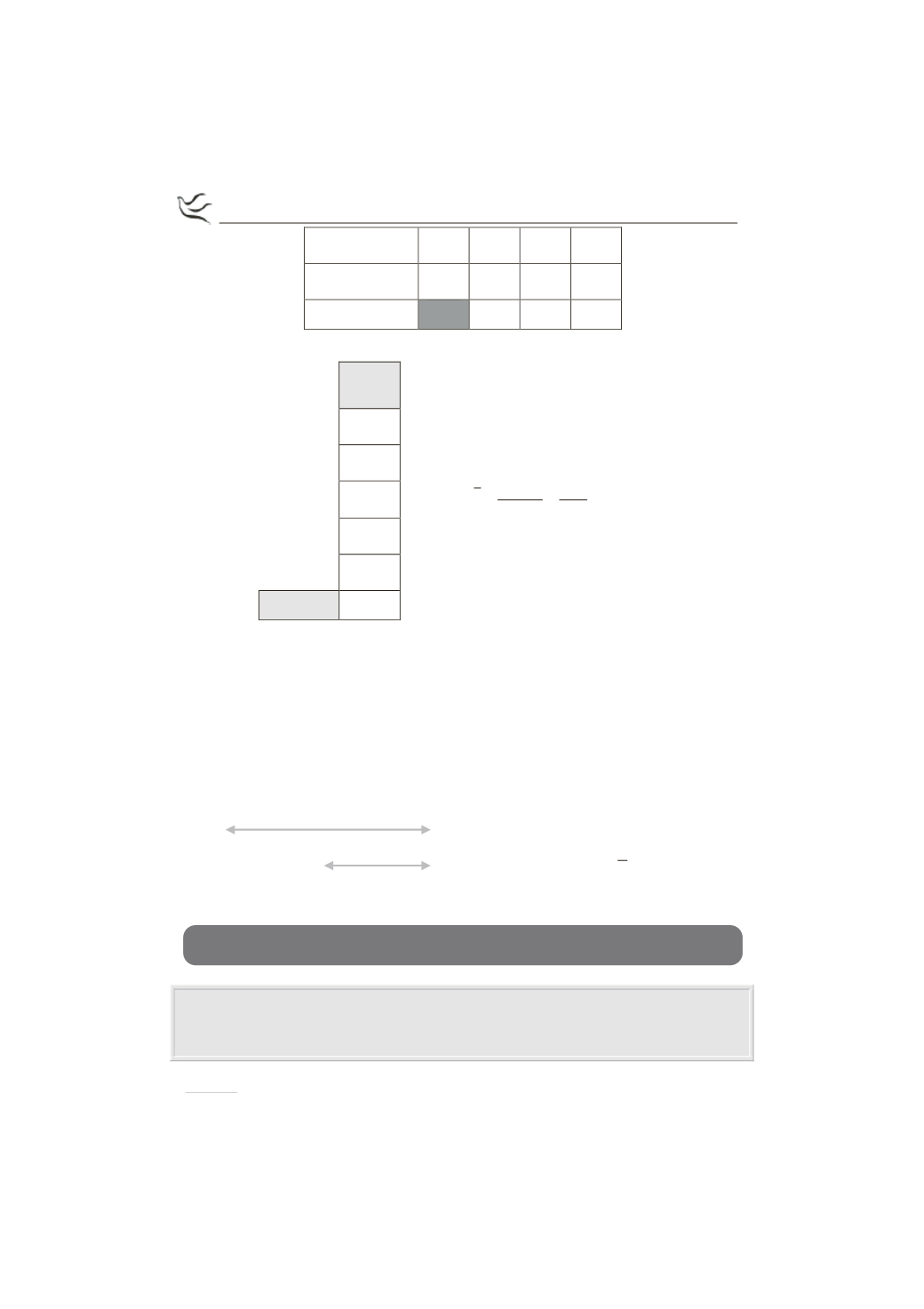
Προσθέτουμε στον παραπάνω πίνακα την παρακάτω στήλη
Β3.
Το ζητούμενο πλήθος είναι
= + =
1 2
κ ν ν 24
μαθητές
Β4.
Το ζητούμενο ποσοστό είναι
¢
¢
= + = +
4
5
4
p f % f % f % 10%
Δεχόμαστε ότι στο εσωτερικό κάθε κλάσης οι παρατηρήσεις κατανέμονται
ομοιόμορφα.
Έτσι λοιπόν είναι:
Το ζητούμενο λοιπόν ποσοστό είναι
=
p 15%
.
Έστω
{
}
=
1 2 3 4
Ω ω ,ω ,ω ,ω
ο δειγματικός χώρος ενός πειράματος τύχης και τα
ενδεχόμενά του
{ }
=
1
3
Α ω ,ω
και
{ }
=
2 4
Β ω ,ω
.
ΘΕΜΑ Γ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2010
Είναι:
=
=
= =
å
5
i i
i 1
x
ν
864
x
14,4
ν
60
i i
x
ν
132
156
360
102
114
Σύνολο
864
Από το διπλανό σχήμα
έχουμε ότι:
¢ = =
4
4
1
f % f % 5%
2
16
18
f
4
%
17
18
f
4
’
%









