Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
172
Αν
( )
( )
f
2
2
P A 1 f P A f
ν
ν
æ ö
< < Û é
ù > ç ÷
ë
û è ø
1
Άρα από την
(3)
έχουμε ότι
( )
( )
( )
- -
= Û = Û = Û - - = Û - - =
2
2
2
Ν A
2
2
ν 9ν 8 2
P A
ν 9ν 8 2 ν 9ν 10 0
ν Ν Ω ν
ν
ν
= + =
Δ 81 40 121
,
±
=
=
1,2
9 11
ν
2
ì
í
-î
10
1
Για
=
ν 10
είναι
( )
( )
= Û =
2
1
P A
P A
10
5
β.
Έτσι λοιπόν
(
)
(
)
(
)
( ) (
)
P
Α Β P Α Β 1 P A B 1 P A P A B
é
ù¢
¢È = - = - - = - é
- Ç ù =
ë
û
ê
ú
ë
û
( ) (
)
= - + Ç = - + = + = + =
1 1 4 1 24 5 29
1 P A P A B 1
5 6 5 6 30 30 30
Α1.
Αν η συνάρτηση
f
είναι παραγωγίσιμη σε ένα διάστημα Δ και
Î
c
, να
αποδείξετε ότι
( )
(
)
( )
¢
¢
×
= ×
c f x c f x
,
Î
x
Δ
(Μονάδες
9)
Α2.
Πότε μια συνάρτηση
f
λέγεται γνησίως φθίνουσα σε διάστημα Δ του
πεδίου ορισμού της;
(Μονάδες
3)
Α3.
Πως ορίζεται ο δειγματικός χώρος ενός πειράματος τύχης;
(Μονάδες
3)
Α4.
Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό
σας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση τη λέξη
Σωστό
, αν
η πρόταση είναι σωστή, ή
Λάθος
, αν η πρόταση είναι λανθασμένη.
α.
Αν οι συναρτήσεις
f, g
έχουν κοινό πεδίο ορισμού το Α, τότε η
ΘΕΜΑ Α
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2010
Απορρίπτεται γιατί
>
ν 2
Α
Β
Ω
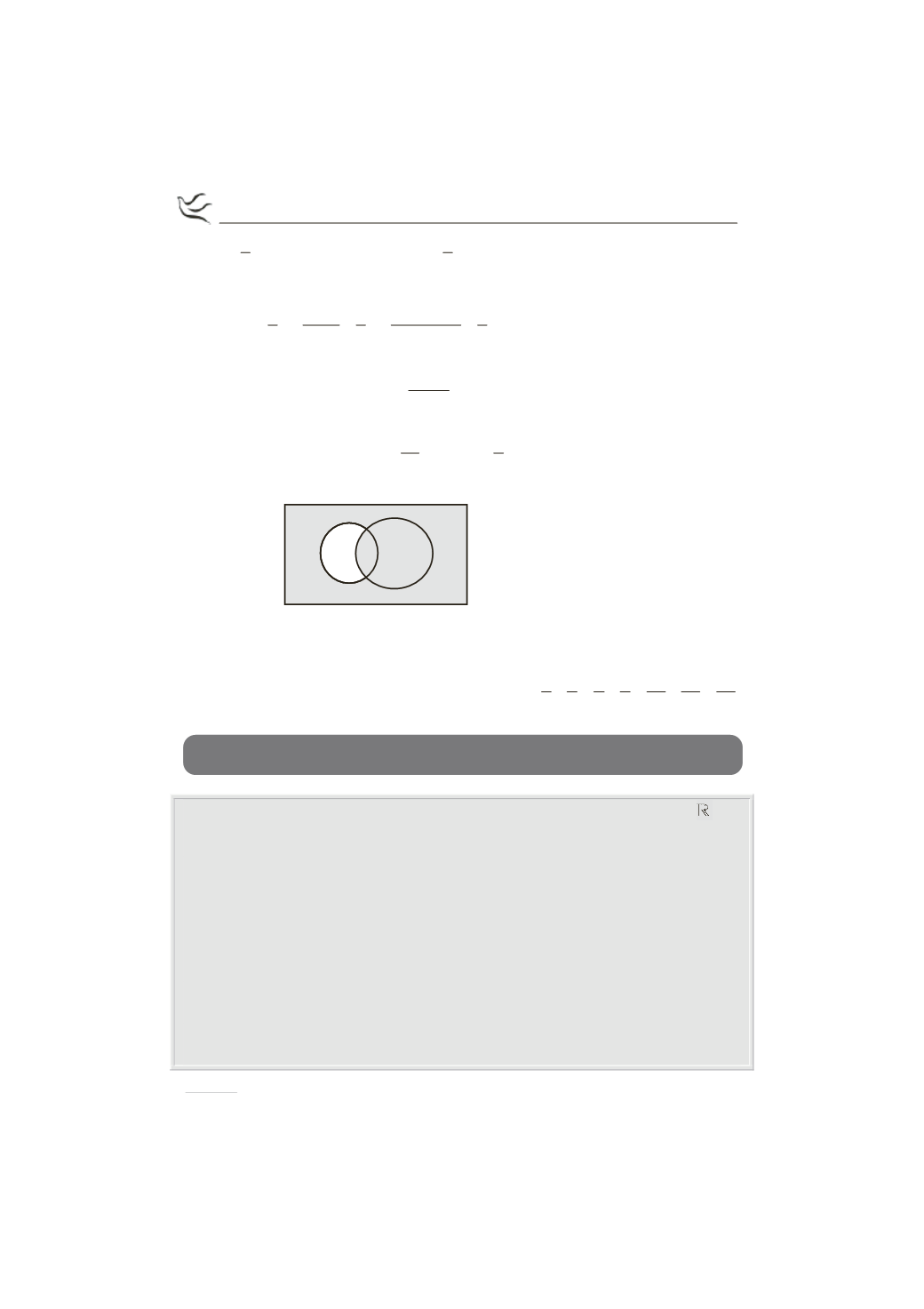
Από το διπλανό
Venn
έχουμε ότι
(
)
¢
¢È -
Α
Β= Α Β









