Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
164
Όμως αφού
< <
0 p 1
είναι
- <
p 1 0
,
<
2
p 1
,
<
3 2
p p
,
2
p p
<
,
+ >
p 1 1
Οπότε
- < < < < +
3 2
p 1 p p p p 1
Έτσι λοιπόν
(
)
Ç =
3
Ρ Α Β p
,
( )
=
2
Ρ Α p
,
(
)
È =
Ρ Α Β p
β.
(
) ( ) ( ) (
)
( )
( )
2
3
3 2
Ρ Α Β Ρ Α P Β Ρ Α Β p p P Β p P Β p p p
È = + - Ç Û = + - Û = - +
γ.
(
) (
)
( ) (
) ( ) (
)
Ρ Β Α Ρ Α Β P Β Ρ Α Β P Α Ρ Α Β
- > - Û - Ç > - Ç Û
Û - + - > - Û - + > Û
3 2
3 2 3
3
2
p p p p p p p 2p p 0
(
)
(
)
>
Û - + > Û - >
p 0
2
2
p p 2p 1 0 p 1 0
(1)
Αλλά
(
)
2
p 1 p 1 0 p 1 0
< Û - < Þ - >
οπότε η
(1)
ισχύει
.
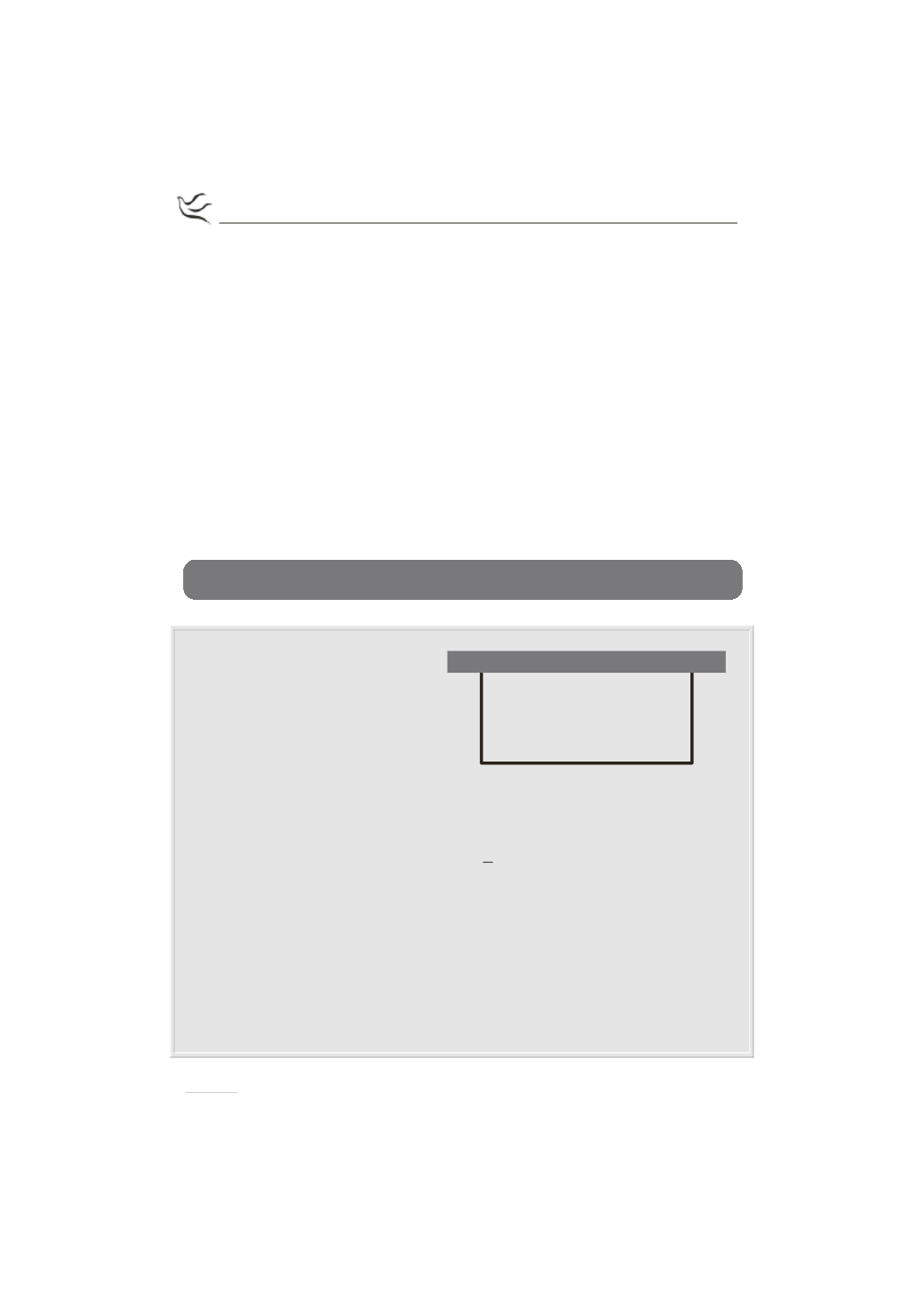
Έχουμε
περιφράξει
με
συρματόπλεγμα μήκους 200
m
μια ορθογώνια περιοχή
από τις τρεις πλευρές της
(Σχήμα 1)
. Η τέταρτη πλευρά
είναι τοίχος. Έστω ότι το
μήκος του τοίχου που θα
χρησιμοποιηθεί είναι
x.
α.
Να αποδείξετε ότι το εμβαδόν της περιοχής που περιφράξαμε δίνεται από
τον τύπο:
( )
= -
2
1
f x 100x x
2
(Μονάδες
6)
β.
Να βρείτε τη μεγαλύτερη δυνατή επιφάνεια που θα μπορούσαμε να
περιφράξουμε με το συρματόπλεγμα των 200
m .
(Μονάδες
7)
γ.
Να βρείτε τη μέση τιμή των αριθμών
( )
¢
f 100
,
( )
¢
f 101
,
(
)
¢
f 102
,
( )
¢
f 103
και
( )
¢
f 104
(Μονάδες
5)
δ.
Έστω
CV
ο συντελεστής μεταβολής των αριθμών
( )
¢
f 100
,
( )
¢
f 101
,
( )
¢
f 102
,
ΘΕΜΑ Δ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2008
Σχήμα 1









