155
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Απάντηση:
α.
Πρέπει
:
- + ¹
2
x x 1 0
,
= - =-
Δ 1 4 3
,
=
f
D
.
β.
Είναι:
( )
®-
®-
-
=
=
= -
- + + +
2
x 1
x 1
x
1
1
lim f x lim
x x 1 1 1 1 3
.
γ.
Η
f
είναι παραγωγίσιμη στο
με παράγωγο:
( )
( )
(
) (
)
(
)
(
)
(
)
¢
¢
- + - - +
- + - ×
-
¢
=
=
=
- +
- +
2
2
2
2
2
2
2
x x x 1 x x
x 1 x x 1 x 2x 1
f x
x x 1
x x 1
-
=
2
x x
+ - +
2
1 2x x
(
)
(
)
-
=
- +
- +
2
2
2
2
2
1 x
x x 1
x x 1
.
Έχουμε διαδοχικά:
( )
¢
= Û - = Û = Û = ±
2
2
f x 0 1 x 0 x 1 x 1
.
Το πρόσημο της
f
΄ εξαρτάται από το πρόσημο του
-
2
1 x
αφού
(
)
- + >
2
2
x x 1 0
για κάθε
Î
x
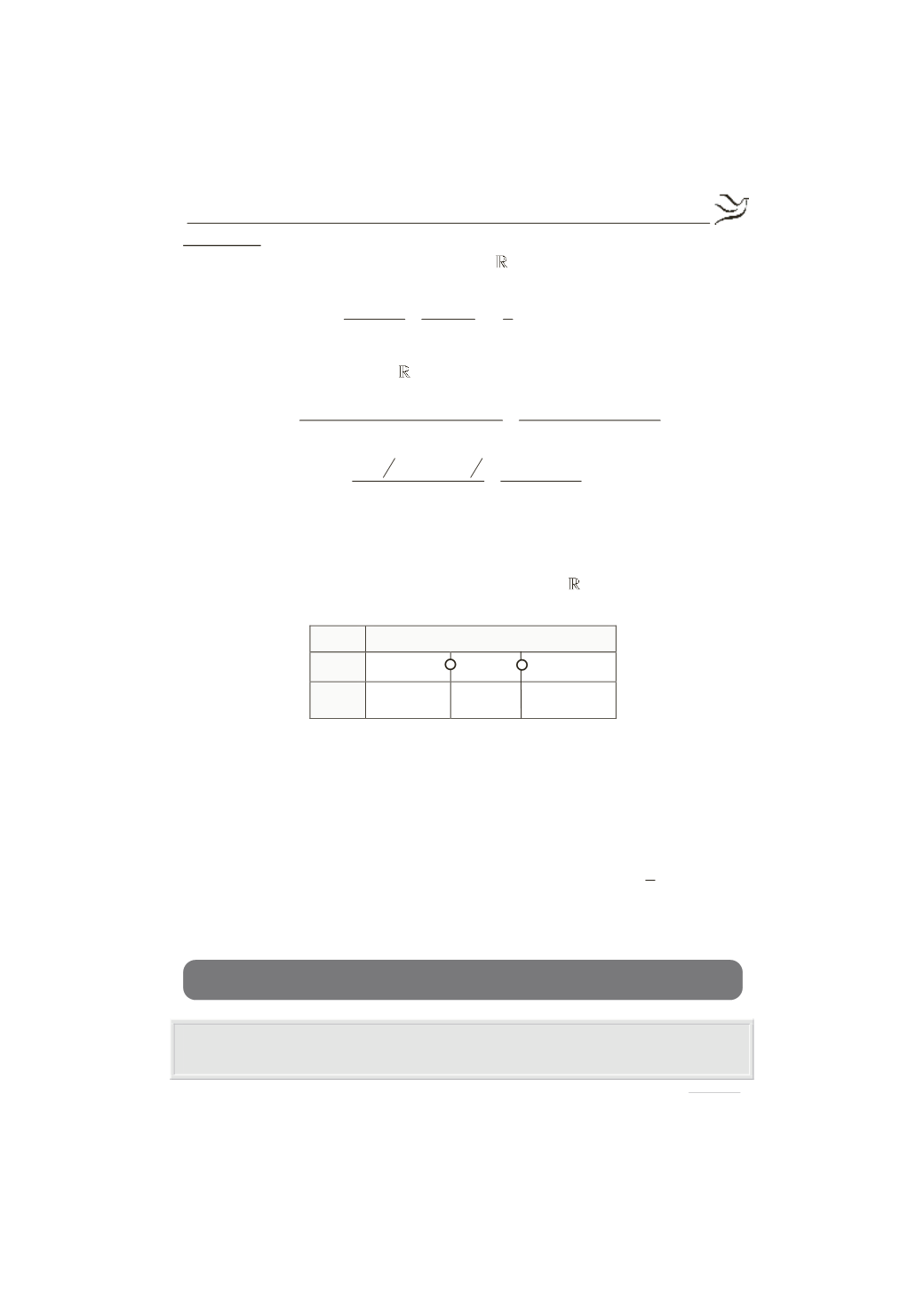
Από τον παραπάνω πίνακα μεταβολών έχουμε:
·
f
γνησίως φθίνουσα στο
(
]
-¥ -
, 1
και στο
[
)
+¥
1,
·
f
γνησίως αύξουσα στο
[
]
-
1,1
·
f
παρουσιάζει τοπικό ελάχιστο στο
= -
1
x 1
με τιμή
( )
- = -
1
f 1
3
·
f
παρουσιάζει τοπικό μέγιστο στο
=
2
x 1
με τιμή
( )
=
f 1
1
Έστω ο δειγματικός χώρος
{
}
=
Ω 1,2,3,4,5
. Θεωρούμε τα ενδεχόμενα Α, Β του
Ω ορίζονται ως εξής:
x
-¥
-
1
1
+¥
( )
¢
f x
-
+
-
f
>
1 >
ΘΕΜΑ Γ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2007
T.M.
T.E.









