Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
148
έχουμε ότι:
2
2
f(2)
e e
= Û
(
)
2
2
α 2 β 2 9 e
× × + × + =
4
α 2β 9 1
Û + + = Û
4
α 2β 8 2α β 4 β 4 2α
Û +
= - Û + = - Û = - -
(1)
Επίσης αφού η ευθεία
= - +
2
2
y e x 3e
είναι εφαπτομένη της γραφικής
παράστασης της συνάρτησης στο σημείο
(
)
2
Α 2,e
έχουμε ότι:
2
2
f (2) e e
¢ = - Û
(
)
2
2
α 2 β 2 2α 2 9 β e
× + × + × + + = - Û
( )
1
4
α 2β 4α 9 β 1 8α 3β 10
Û + + + + = - Û + = - Û
(
)
8
α 3 4 2α
10 8α 12 6α 10
Û + - - = - Û - - = -
2
α 2
α 1
Û = Û =
Για
α 1
=
η
(1)
β 4 2 1 β 6
Û = - - × Û = -
β. Για
α 1
=
και
β 6
= -
η συνάρτηση γράφεται:
(
)
= -
+
x 2
f(x) e x 6x 9
Οπότε:
( ) (
)
(
)
x
2
x 2
f (x) e x 6x 9 e x 6x 9
¢
¢
¢ =
- + + - + =
(
)
(
)
(
)
x 2
x
x 2
e x 6x 9 e 2x 6 e x 6x 2x 9 6
= - + + - = - + + -
Άρα:
(
)
x 2
f (x) e x 4x 3
¢
= - +
(
)
¢
= Û - + = Û - + =
x 2
2
f (x) 0 e x 4x 3 0 x 4x 3 0
( )
2
2
Δ β 4αγ 4 4 1 3 16 12 4
= - = - - × × = - =
( )
1,2
4 4 4 2
x
2 1
2
- - ±
±
=
= =
×
+ì = ïï
í
-ï =
ïî
4 2
3
2
4 2
1
2
Ισχύει ότι
>
x
e 0
για κάθε
Î
x
.
Άρα το πρόσημο της
¢
f (x)
εξαρτάται αποκλειστικά από το πρόσημο του
τριωνύμου
- +
2
x 4x 3
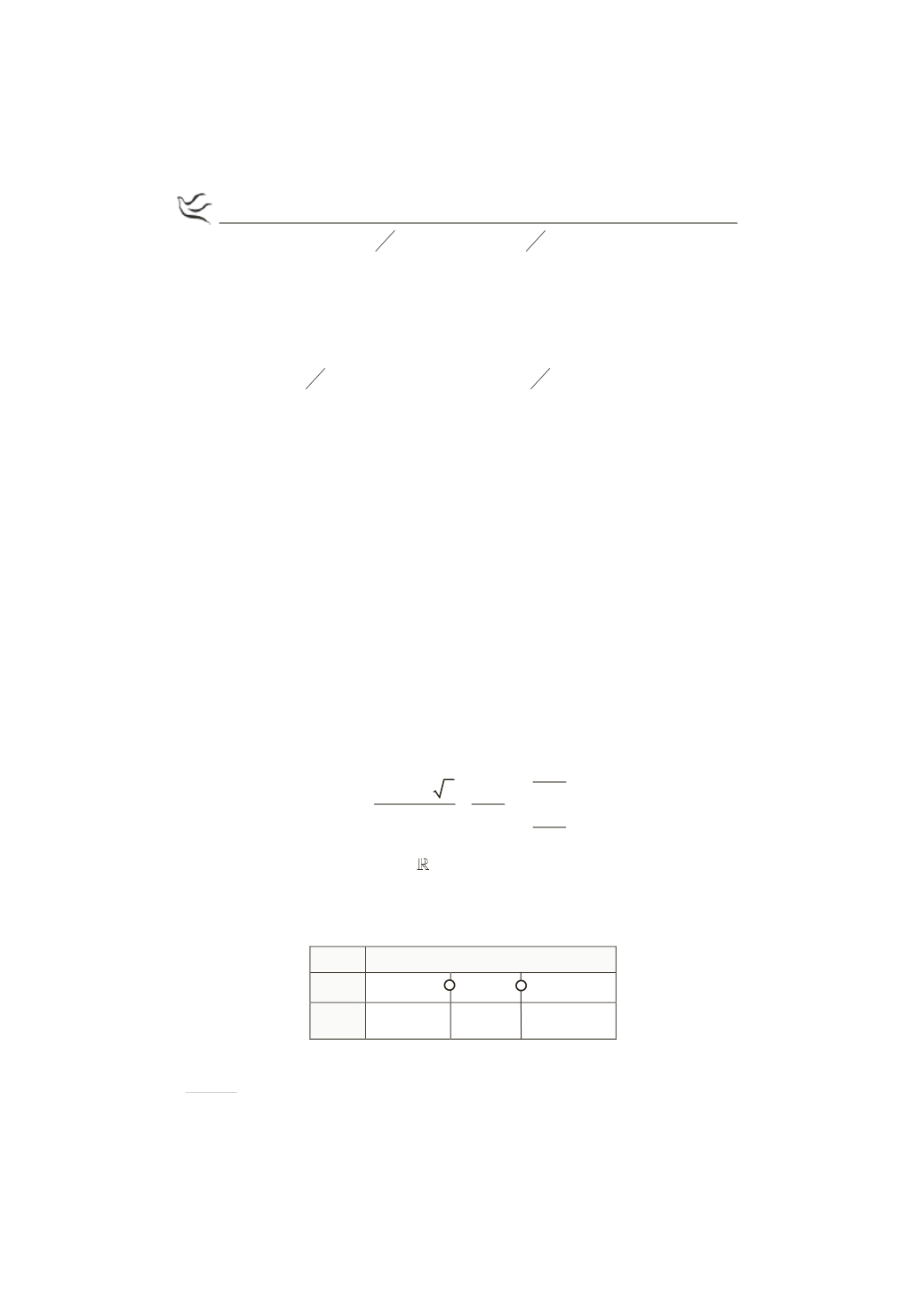
και φαίνεται στο παρακάτω πίνακα:
x
-¥
1
3
+¥
( )
¢
f x
+
-
+
f
1
> 1
T.M.
T.E.









