145
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
( )
( )
Û = + Û =
2 3
5
Ρ Α
Ρ Α
10 10
10
.
(
)
( ) ( ) (
)
È = Û + - Ç = Û
6
6
Ρ Α Β
Ρ Α Ρ Β Ρ Α Β
10
10
( )
( )
5
3 6
4
Ρ Β
Ρ Β
10
10 10
10
Û + - = Û =
.
Επιπλέον
+
ì
ü
= Î
³
í
ý
-
î
þ
x 1
Γ x Ω /
2
x 1
.
Για
¹
x 1
είναι
(
)
Î ¹
>
+
³ Û + ³ - Û + ³ - Û £
-
x Ω, x 1
x 1
x 1
2
x 1 2 x 1 x 1 2x 2 x 3
x 1
.
Άρα
{
}
= Î £
¹
Γ x Ω / x 3 και x 1
δηλαδή
{ }
=
Γ 2,3
οπότε
( )
( )
(
)
= =
Ν Γ 2
Ρ Γ
Ν Ω 10
.
β.
Το ενδεχόμενο να πραγματοποιηθεί το Β και όχι το Γ είναι το
:
{ }
- =
Β Γ 1,4,5
άρα
(
) (
)
( )
-
- =
=
W
Ν Β Γ 3
Ρ Β Γ
Ν 10
.
γ.
Είναι
{ }
- =
Γ Β 2
.
Το ενδεχόμενο να πραγματοποιηθεί μόνο ένα από τα Β και Γ είναι το
(
) (
) {
}
Β Γ Γ Β 1,2,4,5
- È - =
,
άρα
(
) (
)
(
) (
)
( )
Ν Β Γ Γ Β 4
Ρ Β Γ Γ Β
Ν
10
é - È - ù
ë
û
é - È - ù =
=
ë
û
W
.
δ.
Η μέση τιμή των λ, 3λ, 5λ είναι
+ +
=
=
λ 3λ 5λ
x
3λ
3
.
Οπότε
(
) (
) (
) (
)
=
-
- + - + -
+
=
=
=
=
å
3
2
2
2
2
2
2
2
i
2 i 1
t x
λ 3λ 3λ 3λ 5λ 3λ 4λ 4λ 8λ
s
3
3
3
3
.
1
4
5
2
6
7
8
9
10
Α
Ω
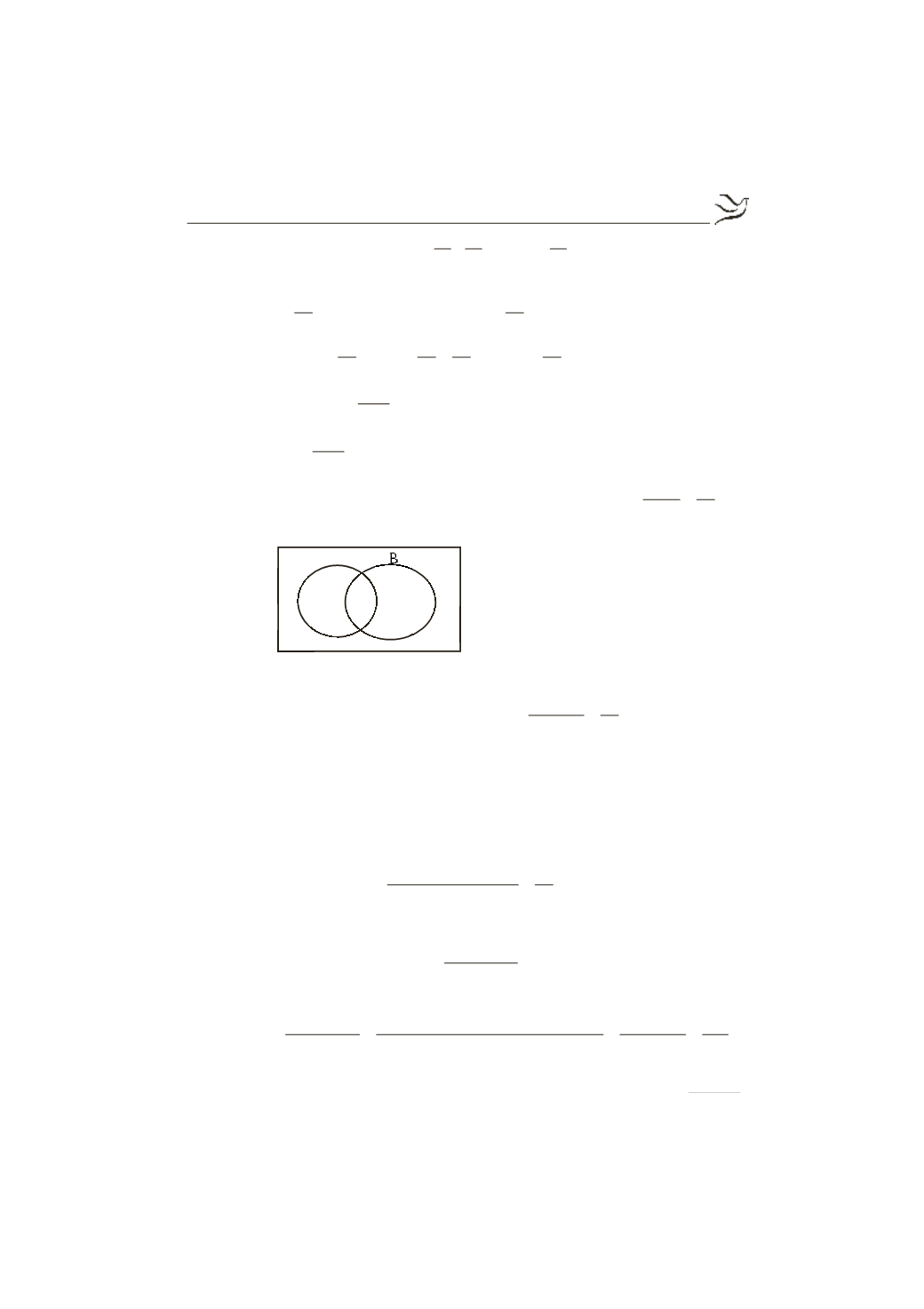
Από το διπλανό διάγραμμα
Venn
έχουμε ότι
:
{
}
Α= 1,2,3,4,6
{
}
Β= 1,3,4,5
3









