143
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
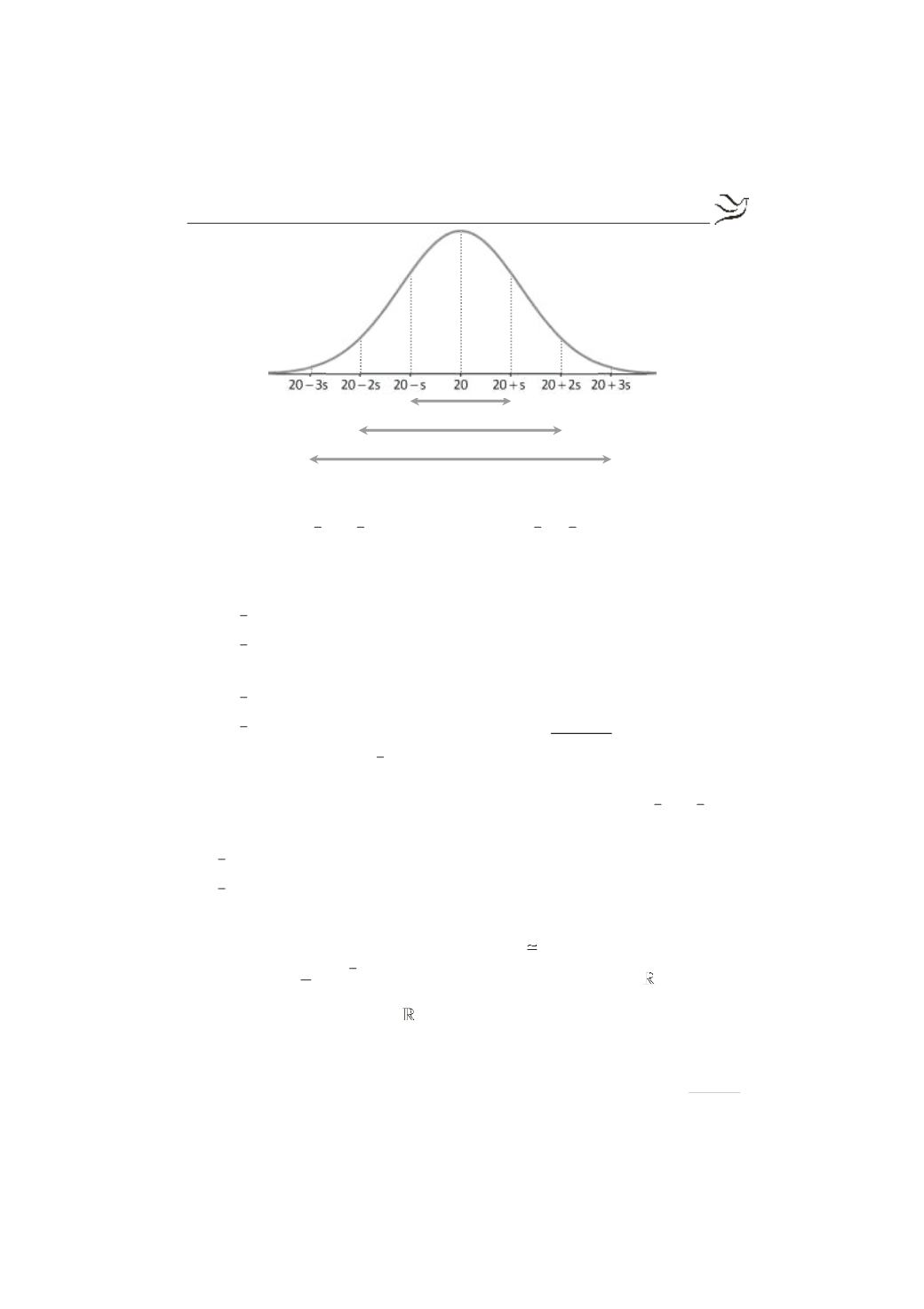
Από το παραπάνω σχήμα έχουμε ότι το 81,5% των παρατηρήσεων βρίσκεται
στο διάστημα
(
)
- +
x 2s,x s
και στο διάστημα
(
)
- +
x s,x 2s
.
Έτσι λοιπόν έχουμε ότι:
ì - = ï
í
+ = ïî
x 2s 16
x s 22
Û
- =
ì
í
+ = î
20 2s 16
20 s 22
Û
=ì
í
=î
s 2
s 2
Û
=
s 2
ή
ì - = ï
í
+ = ïî
x s 16
x 2s 22
Û
- = ì
í
+ =
î
20 s 16
20 2s 22
Û
=ì
í
=î
s 4
s 1
Αδύνατο
Έτσι λοιπόν
=
s 2
και
=
x 20
β)
Το 95% περίπου των παρατηρήσεων βρίσκεται στο διάστημα
(
)
- +
x 2s,x 2s
δηλαδή στο διάστημα (16,24). Οπότε έχουμε:
ì - = ï
í
+ = ïî
x αs 16
x αs 24
Û
- =
ì
í
+ =
î
20 2α 16
20 2α 24
Û
= ì
í
= î
2α 4
2α 4
Û
=
α 2
γ)
Αφού έχουμε κανονική κατανομή ισχύει ότι
=
R 6s 12
Οπότε
( )
(
)
( )
2
2
R
f x x x 4 x 9s f x 6x 24x 18
2
= - + + Û = - +
με
Î
x
Είναι
( )
¢
= -
f x 12x 24
με
Î
x
·
( )
f x 0 12x 24 0 12x 24 x 2
¢
= Û - = Û = Û =
0,15%
34%
34%
13,5%
13,5%
2,35%
2,35%
0,15%
68%
95%
99,7%









