Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
98
γ)
Αν μια συνάρτηση f δεν είναι συνεχής στο
0
x
, τότε η
f
δεν είναι πα-
ραγωγίσιμη στο
0
x
.
δ)
Υπάρχει πολυωνυμική συνάρτηση βαθμού
ν 2
³
, η οποία έχει ασύ-
μπτωτη.
ε)
Για κάθε συνάρτηση
f
, συνεχή στο
[ ]
α,β
, ισχύει:
αν
( )
>
ò
β
α
f x dx 0
, τότε
( )
f x 0
>
στο
[ ]
α,β
.
Μονάδες 10
Απάντηση
Α1.
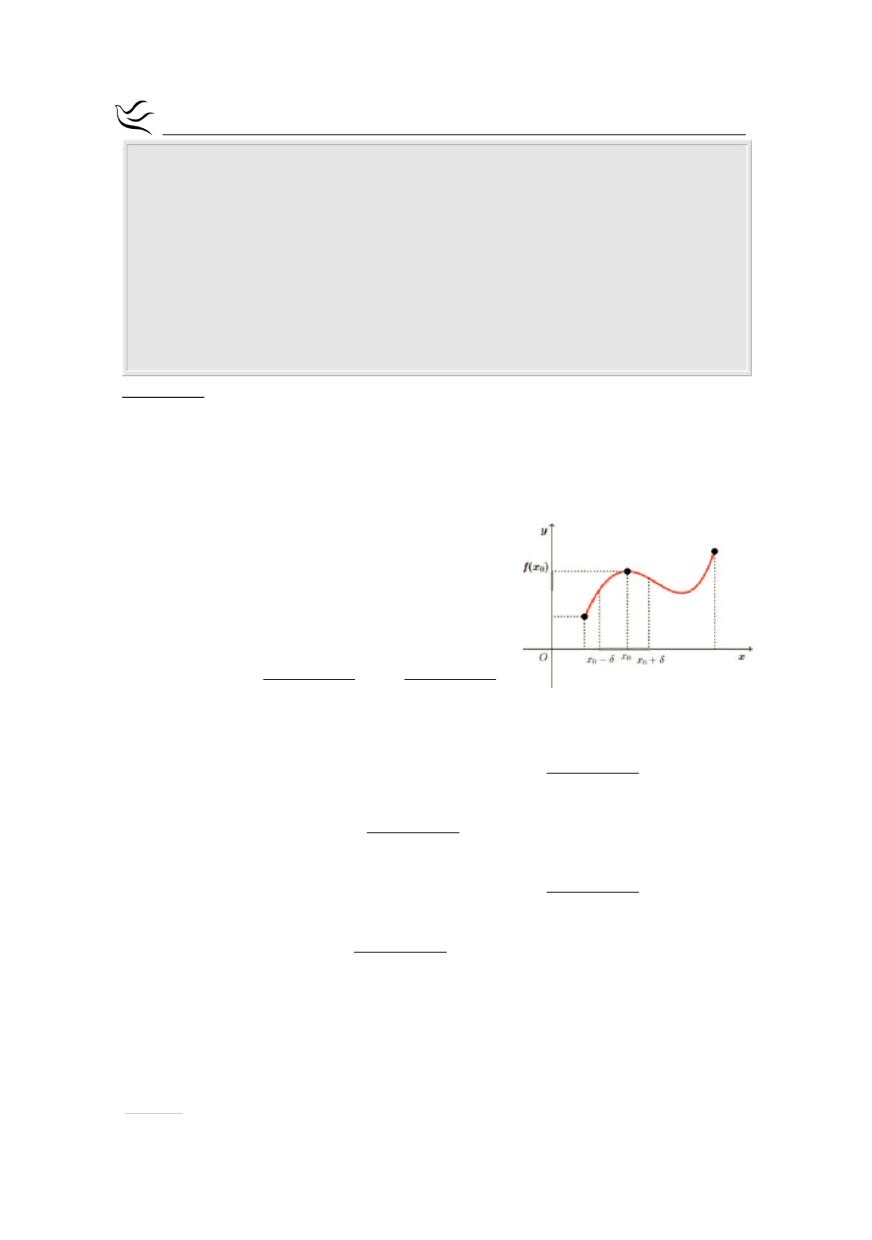
Ας υποθέσουμε ότι η
f
παρουσιάζει στο
0
x
τοπικό μέγιστο. Επειδή το
0
x
είναι εσωτερικό σημείο του Δ και η
f
παρουσιάζει σ’ αυτό τοπικό μέγιστο,
υπάρχει
δ 0
>
τέτοιο, ώστε:
(
)
0
0
x δ,x δ Δ
- + Í
και
( ) ( )
0
f x f x
£
για κάθε
(
)
0
0
x x δ,x δ
Î - +
(1).
Επειδή, επιπλέον, η
f
είναι παραγωγίσιμη
στο
0
x
, ισχύει
( )
( ) ( )
( ) ( )
0
0
0
0
0
x x
x x
0
0
f x f x
f x f x
f x lim
lim
x x
x x
-
+
®
®
-
-
¢
=
=
-
-
Επομένως,
·
αν
(
)
0
0
x x δ,x
Î -
τότε λόγω της
(1)
, θα είναι
( ) ( )
0
0
f x f x
0
x x
-
³
-
, οπότε θα
έχουμε :
( )
( ) ( )
0
0
0
x x
0
f x f x
f x lim
0
x x
-
®
-
¢
=
³
-
(2)
·
αν
(
)
0 0
x x ,x δ
Î +
τότε λόγω της
(1)
, θα είναι
( ) ( )
0
0
f x f x
0
x x
-
£
-
, οπότε θα
έχουμε:
( )
( ) ( )
0
0
0
x x
0
f x f x
f x lim
0
x x
+
®
-
¢
=
£
-
(3)
Έτσι, από τις
(2)
και
(3)
έχουμε:
( )
0
f x 0
¢
=









