Μαθηματικά Γ' Λυκείου

Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ

. Θεώρημα

Γεωμετρική ερμηνεία του Θεώρηματος

Rolle

Γεωμετρικά, αυτό σημαίνει ότι υπάρχει

ένα, τουλάχιστον,

( )

ξ α,β

τέτοιο, ώ-

στε η εφαπτομένη της

στο

( )

(

)

ξ,f ξ

να είναι παράλληλη στον

άξονα των x΄

Θεώρημα Μέσης Τιμής

Αν μια συνάρτηση

είναι

συνεχής στο κλειστό διάστημα

[ ]

α,β

παραγωγίσιμη στο ανοικτό διάστημα

( )

α,β

τότε υπάρχει ένα, τουλάχιστον

( )

ξ α,β

τέτοιο ώστε

( ) ( ) ( )

β f α

β α

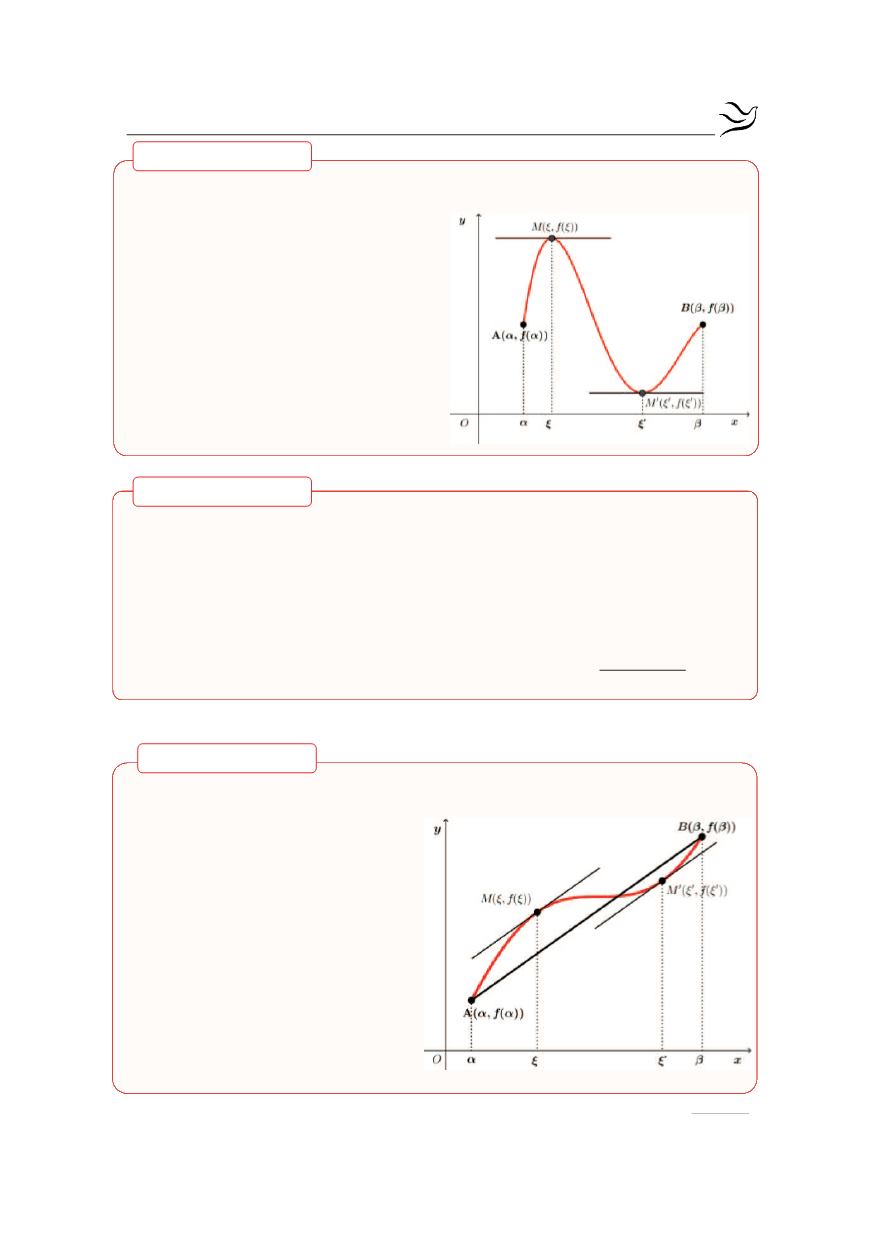
Γεωμετρική Ερμηνεία του Θεωρήματος Μέσης Τιμής

Γεωμετρικά, αυτό σημαίνει ότι υ-

πάρχει ένα, τουλάχιστον,

( )

ξ α,β

τέτοιο, ώστε η εφαπτομένη της

γραφικής παράστασης της f στο

σημείο

( )

(

)

ξ,f ξ

να είναι παράλ-

ληλη του ευθύγραμμου τμήματος

ΑΒ.