Μαθηματικά Γ' Λυκείου

33 / 368

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
32
20. Ορισμός
21. Ορισμός
19. Θεώρημα
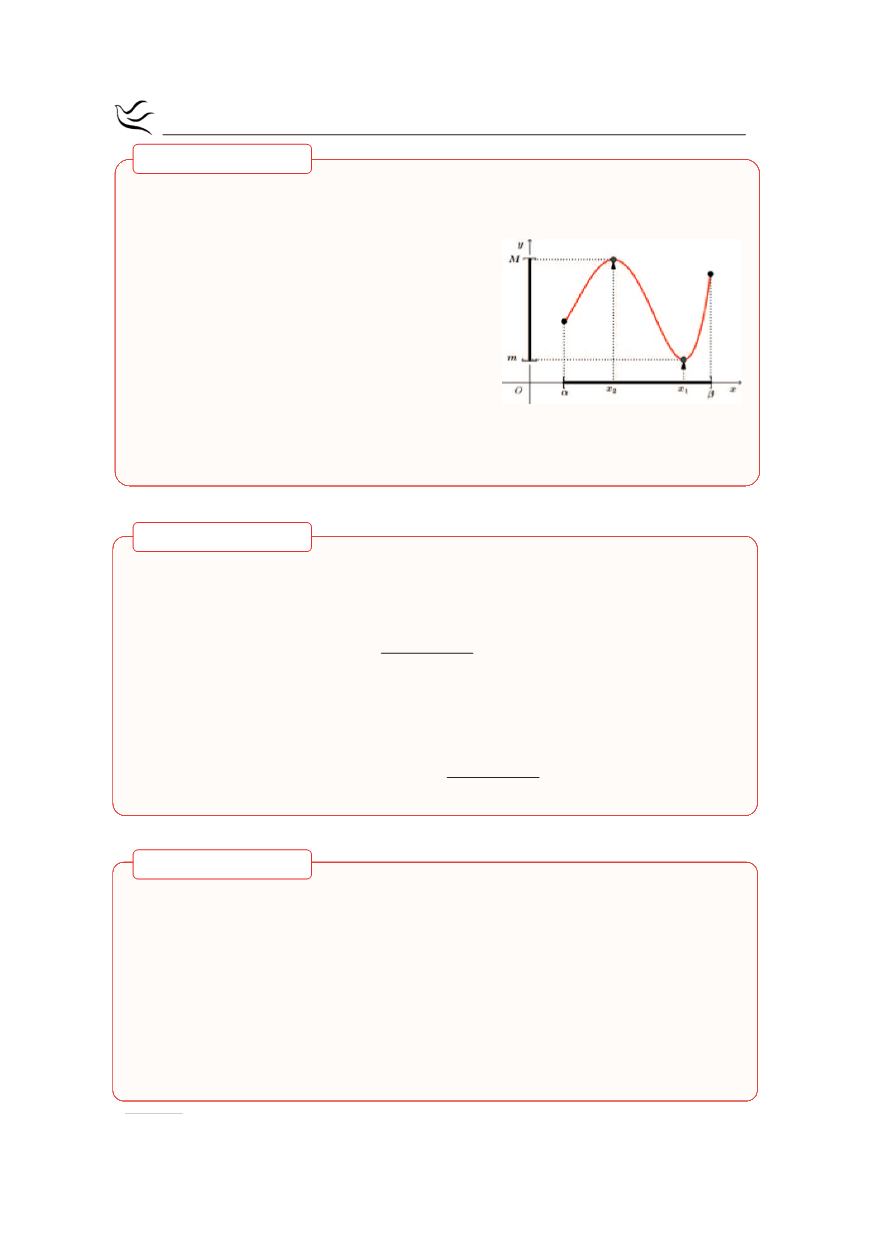
Θεώρημα Μέγιστης και Ελάχιστης Τιμής
Αν f είναι συνεχής συνάρτηση στο [ ]α,β ,
τότε η f παίρνει στο [ ]α,β μια μέγιστη τιμή
Μ και μια ελάχιστη τιμή m.
Δηλαδή, υπάρχουν [ ]
1 2 x ,x α,β Î τέτοια, ώστε,
αν ( )1 m f x= και ( )2 M f x= , να ισχύει
( )
m f x M£ £ , για κάθε [ ]α β x ,Î .
Παράγωγος της f στο 0
x
Μια συνάρτηση f λέμε ότι είναι παραγωγίσιμη σ’ ένα σημείο 0 x του πεδίου
ορισμού της, αν υπάρχει το
( ) ( )
0
0
x x
0
f x f x
lim
x x ®
-
-
και είναι πραγματικός αριθμός.
Το όριο αυτό ονομάζεται παράγωγος της f στο 0 x και συμβολίζεται με ( )0 f x¢ .
( Lagrange)
Δηλαδή: ( ) ( ) ( )
0
0
0 x x
0
f x f x
f x lim
x x ®
-
¢ =
-
.
Παράγωγος της f σε διάστημα
Έστω f μια συνάρτηση με πεδίο ορισμού ένα σύνολο Α. Θα λέμε ότι:
P H f είναι παραγωγίσιμη στο Α ή παραγωγίσιμη, όταν είναι παραγωγί-
σιμη σε κάθε σημείο 0 x AÎ .
P Η f είναι παραγωγίσιμη σε ένα ανοικτό διάστημα ( )α,β του πεδίου
ορισμού της, όταν είναι παραγωγίσιμη σε κάθε σημείο ( )
0 x α,β Î .