29
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
11. Ορισμός
2
.
( )
(
)
( )
0
0
x x
x x
lim
κf x κ lim f x
®
®
=
,για κάθε σταθερά
κ
Î
3.
( ) ( )
(
)
( )
( )
0
0
0
x x
x x
x x
lim f x g x lim f x lim g x
®
®
®
×
=
×
4.
( )
( )
( )
( )
0
0
0
x x
x x
x x
lim f x
f x
lim
g x lim g x
®
®
®
=
, εφόσον
0
x x
lim g(x) 0
®
¹
5.
( )
( )
0
0
x x
x x
lim f x lim f x
®
®
=
6.
( )
( )
0
0
k
k
x x
x x
lim f x lim f x
®
®
=
,
εφόσον
( )
f x 0
³
κοντά στο
0
x
.
7.
( )
( )
0
0
ν
ν
x x
x x
lim f x
lim f x
®
®
é
ù
é ù =
ë û ê
ú
ë
û
,
*
ν
Î
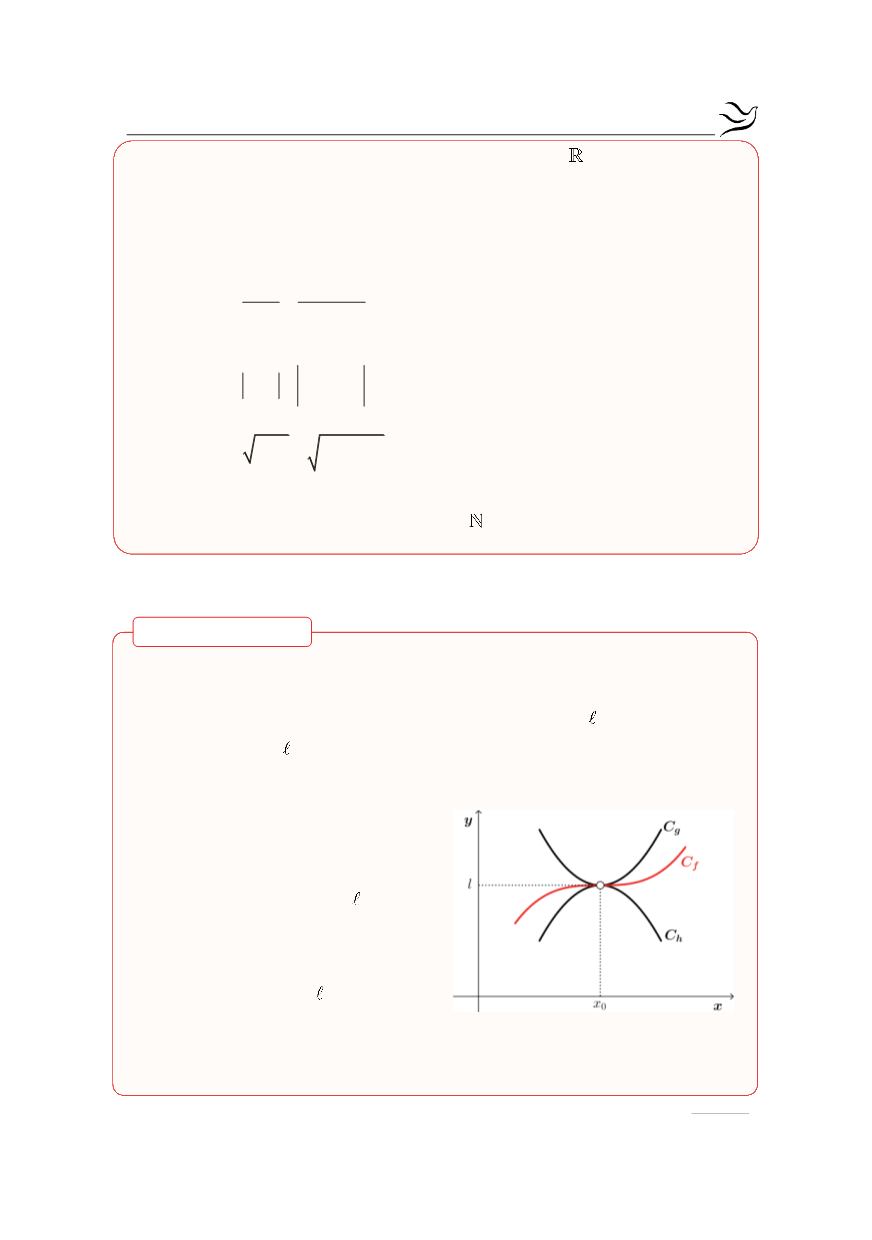
Κριτήριο παρεμβολής
Θεωρούμε μια συνάρτηση
f
“εγκλωβισμένη” σε μια περιοχή του
0
x
ανάμεσα
σε δύο συναρτήσεις h και g. Αν οι h και g έχουν κοινό όριο στο
0
x
, τότε και η
f
θα έχει το ίδιο όριο
.
Επομένως, αν
P
( ) ( ) ( )
h x f x g x
£ £
κοντά στο
0
x
και
P
( )
( )
0
0
x x
x x
limh x lim g x
®
®
=
=
τότε υπάρχει
το όριο της
f
στο
0
x
και
( )
0
x x
lim f x
®
=









