25
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
1. Ορισμός
Ορισμοί
Πραγματική συνάρτηση
-
Πεδίο ορισμού
-
Σύνολο τιμών
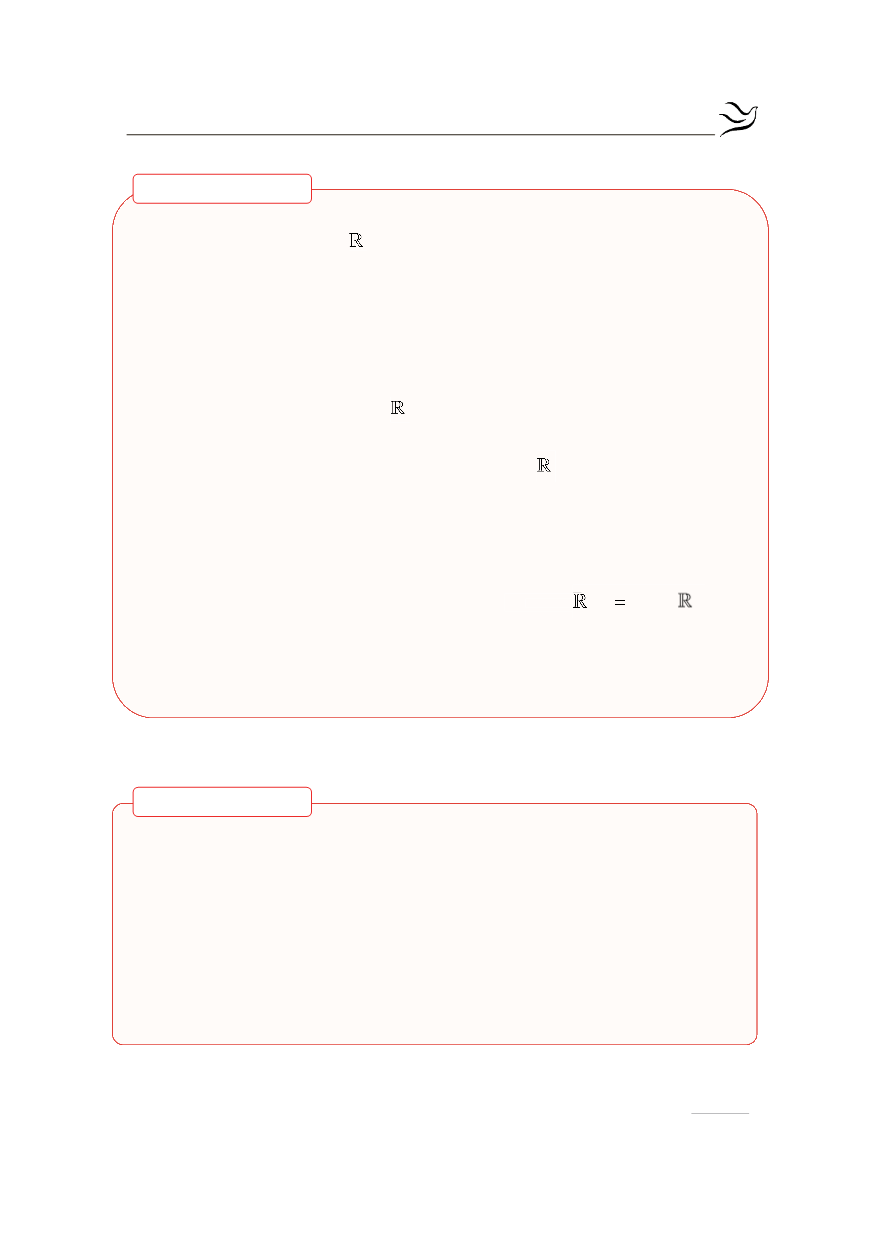
Έστω Α ένα υποσύνολο του . Ονομάζουμε
πραγματική συνάρτηση
με
πεδίο
ορισμού το Α
μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο
x A
Î
α-
ντιστοιχίζεται σε ένα μόνο πραγματικό αριθμό y. Το y ονομάζεται
τιμή της f
στο x
και συμβολίζεται με
( )
f x
.
Η διαδικασία αυτή περιγράφεται αν γράψουμε:
®
f:A
( )
x f x
®
P
Ανεξάρτητη μεταβλητή
ονομάζουμε το x
Α
Î
.
P
Εξαρτημένη μεταβλητή
ονομάζουμε το
( )
y f x
= Î
.
P
Πεδίο ορισμού
είναι το σύνολο Α. Αν η συνάρτηση δίνεται μόνο με τον τύ-
πο της, τότε ως πεδίο ορισμού θεωρούμε το
ευρύτερο
υποσύνολο
των
πραγματικών αριθμών
x
για το οποίο η τιμή
( )
f x
έχει νόημα πραγματικού
αριθμού.
Το πεδίο ορισμού συμβολίζεται με
f
D
, όπου
( )
{
}
f
D x / y f x
= Î = Î
.
P
Σύνολο τιμών
ονομάζουμε το σύνολο που έχει για στοιχεία του
,
τις τιμές
(εικόνες) της f για όλα τα
Î
x A
και συμβολίζεται με
( )
f A
, όπου:
( )
( )
{
}
f A y / y f x
για κάποιο x A
= =
Î
2.
Ορισμός
Γραφική Παράσταση Συνάρτησης
Γραφική παράσταση
της f που συμβολίζουμε με
f
C
ονομάζουμε το σύνολο των
σημείων
( )
M x,y
για τα οποία ισχύει
( )
y f x
=
. Ισχύει δηλαδή:
( )
(
)
{
}
f
C M x,f x / x A
=
Î
Εξίσωση της γραφικής παράστασης της f
ονομάζουμε την εξίσωση
( )
y f x
=
που επαληθεύεται μόνο από τα σημεία της
f
C
.









