Μαθηματικά Γ' Λυκείου

31 / 368

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
30
12. Ορισμός
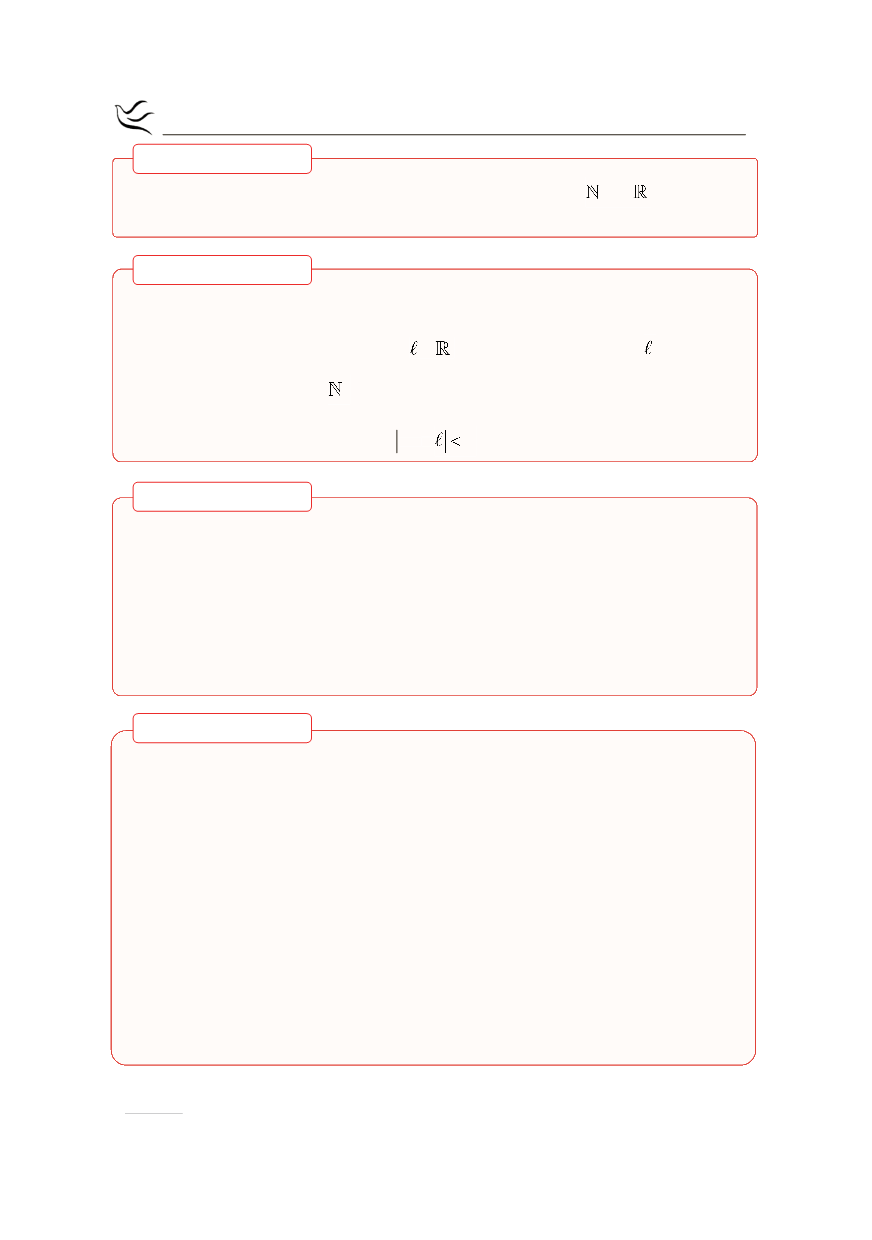
Μια ακολουθία ( )ν α έχει όριο το Î και γράφουμε ν
ν
limα
®¥
= , όταν για
κάθε ε 0> , υπάρχει *
0 ν Î τέτοιο, ώστε για κάθε 0 ν ν> να ισχύει
ν α ε- <
13. Ορισμός
14. Ορισμός
15. Ορισμός
Ακολουθία ονομάζεται κάθε πραγματική συνάρτηση α *
: ® .
Πεπερασμένο όριο ακολουθίας
Συνέχεια συνάρτησης σε σημείο
Έστω μια συνάρτηση f και 0 x ένα σημείο του πεδίου ορισμού της. Η f θα εί-
ναι συνεχής στο x 0 , όταν
( ) ( )
0
0
x x
lim f x f x
®
=
Συνέχεια συνάρτησης σε διάστημα
P Μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα ανοικτό διάστημα
( )α,β , όταν είναι συνεχής σε κάθε σημείο του ( )α,β .
P Μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα κλειστό διάστημα
[ ]α,β , όταν είναι συνεχής σε κάθε σημείο του ( )α,β και επιπλέον
( ) ( )
x α
lim f x f α
+
®
= και ( ) ( )
x β
lim f x f β
-
®
= .