Μαθηματικά Γ' Λυκείου

27 / 368

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
26
3. Ορισμός
Ισότητα συναρτήσεων
Δύο συναρτήσεις f και g λέγονται ίσες και γράφουμε f g= όταν:
P έχουν το ίδιο πεδίο ορισμού Α και
P για κάθε x AÎ ισχύει ( ) ( )
f x g x= .
4. Ορισμός
Πράξεις συναρτήσεων
Έστω οι συναρτήσεις f, g όπου f : Α ® και g :B ® . Ορίζουμε:
P άθροισμα +
f g : ( )( ) ( ) ( )
f g x f x g x+ = + , Î Ç
x A B
P διαφορά -
f g : ( )( ) ( ) ( )
f g x f x g x- = - , Î Ç
x A B
P γινόμενο f g : ( )( ) ( ) ( )f g x f x g x× = × , Î Ç
x A B
P πηλίκο
f
g
: ( ) ( )
( )
f x f
x
g g x
æ ö
= ç ÷
è ø
, ( ) { }
x A B / g x 0Î Ç ¹
5. Ορισμός
Σύνθεση συναρτήσεων
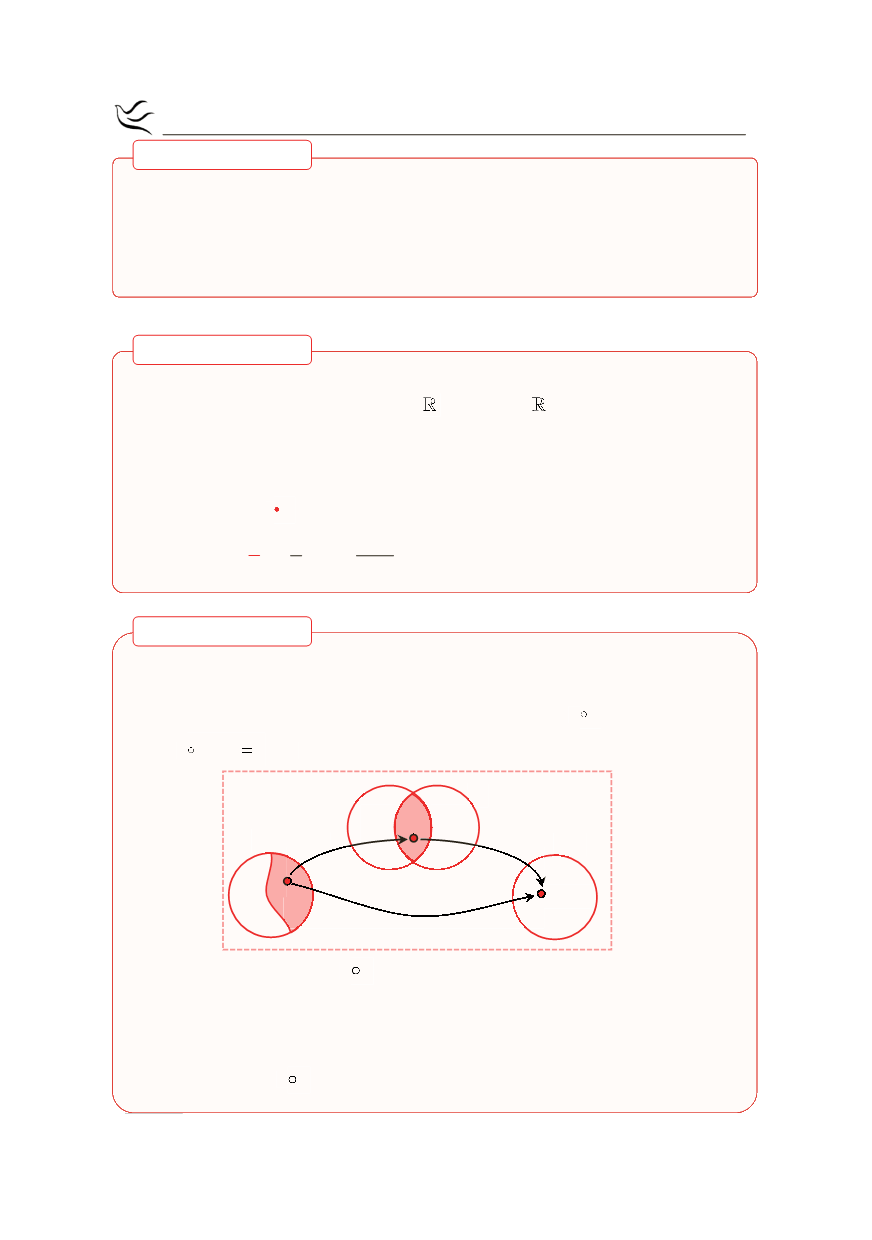
Αν f, g είναι δύο συναρτήσεις με πεδίο ορισμού Α, Β αντίστοιχα, τότε ονομά-
ζουμε σύνθεση της f με την g, και τη συμβολίζουμε με g f , τη συνάρτηση με
τύπο ( )( ) ( ) ( )
g f x g f x=
Το πεδίο ορισμού 1 A της g f αποτελείται από όλα τα στοιχεία x του πεδίου
ορισμού της f για τα οποία το ( )
f x ανήκει στο πεδίο ορισμού της g. Δηλαδή:
( ) { }
1 A x A / f x B= Î Î .
Είναι φανερό ότι η g f ορίζεται αν ¹ Æ
1 A , δηλαδή αν ( )
f A BÇ ¹Æ .
A
A1
g(B)
f(A)
f(x)
g(f(x))
gof
g
f
B