Μαθηματικά Γ' Λυκείου

32 / 368

31
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
16. Θεώρημα
18. Θεώρημα
17. Θεώρημα
Διατύπωση Θεώρηματος Bolzano
Έστω μια συνάρτηση f , ορισμένη σε ένα κλειστό διάστημα [α,β] . Αν:
P η f είναι συνεχής στο [ ]α,β και, επιπλέον, ισχύει
P ( ) ( )
f α f β 0× < ,
τότε υπάρχει ένα, τουλάχιστον, ( )
0 x α,β Î τέτοιο, ώστε ( )0 f x 0= .
Δηλαδή, υπάρχει μια, τουλάχιστον, ρίζα της εξίσωσης ( )
f x 0= στο ανοικτό
διάστημα ( )α,β .
Γεωμετρική Ερμηνεία Θεώρηματος Bolzano
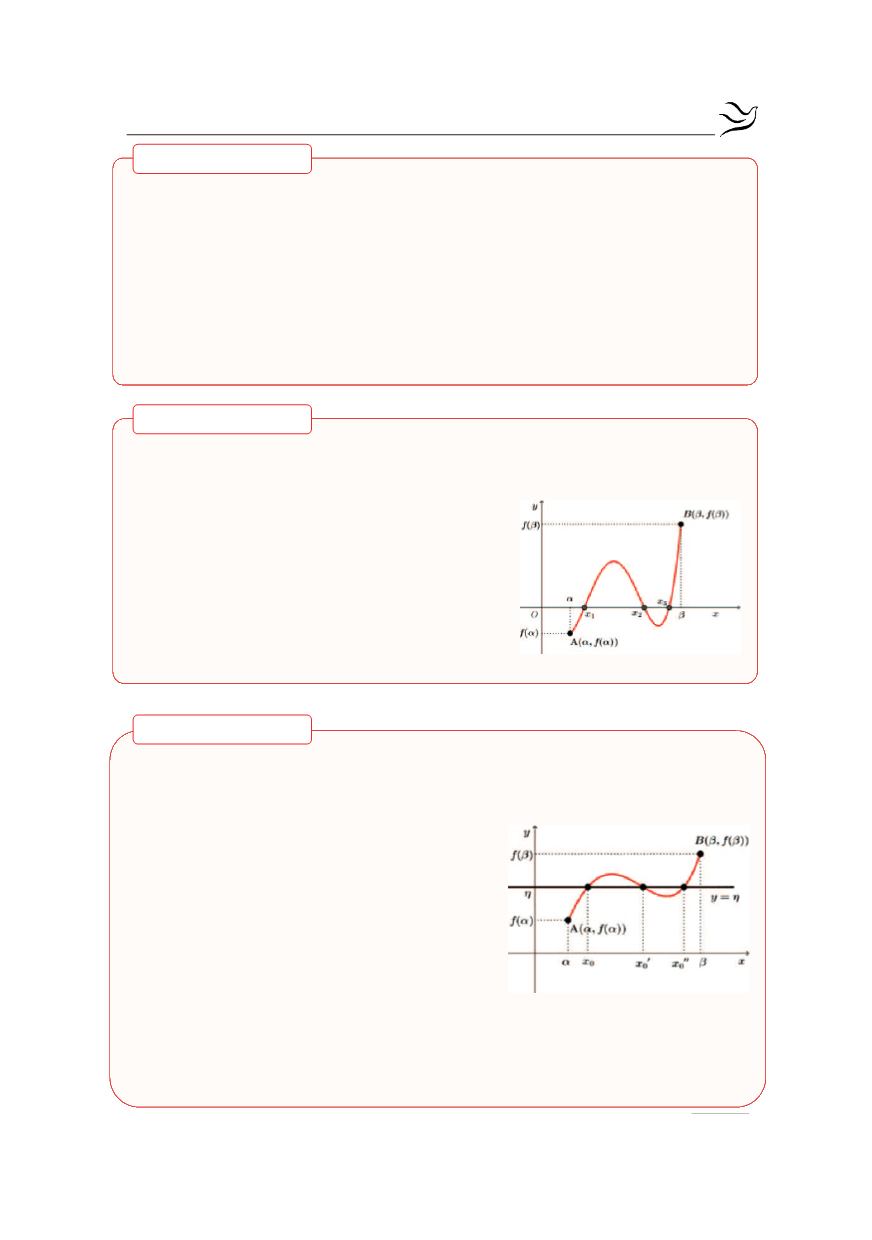
Δίνεται η γραφική παράσταση μιας συνεχούς
συνάρτησης f στο [ ]α,β . Επειδή τα σημεία
( ) ( )
A α,f α και ( ) ( )
B β,f β βρίσκονται εκατέρω-
θεν του άξονα x x¢ , η γραφική παράσταση της f
τέμνει τον άξονα σε ένα τουλάχιστον σημείο.
Θεώρημα ενδιάμεσων τιμών
Έστω μια συνάρτηση f, η οποία είναι ορισμένη σε ένα κλειστό διάστημα [ ]α,β
Αν:
P η f είναι συνεχής στο [ ]α,β και
P ( ) ( )
f α f β¹
τότε, για κάθε αριθμό η μεταξύ των ( )
f α και
( )
f β υπάρχει ένας, τουλάχιστον ( )
0 x α,β Î
τέτοιος, ώστε ( )0 f x η = .
Γεωμετρική ερμηνεία
Αν f συνεχής συνάρτηση στο [ ]α,β και τα σημεία ( ) ( )
A α,f α και ( ) ( )
Β β,f β βρί-
σκονται εκατέρωθεν της ευθείας y η = τότε η f C τέμνει την ευθεία y η = σε ένα
τουλάχιστον σημείο ( )
0 Μ x ,η , με τετμημένη ( )
0 x α,β Î .