Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
28
( )
g:f
Α
®
για την οποία κάθε
( )
y f A
Î
να αντιστοιχίζεται στο μοναδικό
x A
Î
για το ο-
ποίο ισχύει
( )
f x y
=
.
Έτσι η g:
P
έχει πεδίο ορισμού το σύνολο τιμών
( )
f A
της f,
P
έχει σύνολο τιμών το πεδίο ορισμού Α της f και
P
ισχύει η ισοδυναμία
( )
( )
f x y g y x
= Û =
.
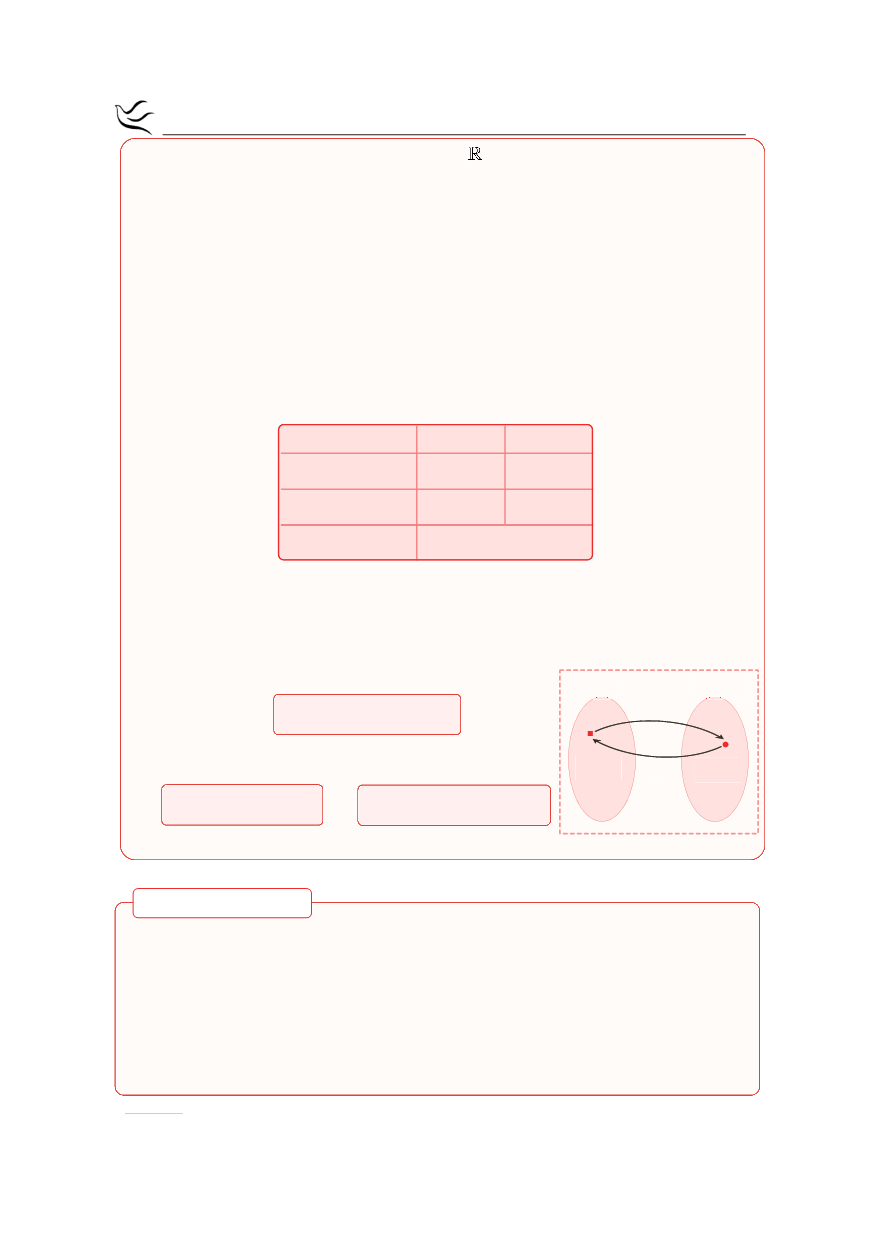
Σχηματικά:
f
g
Πεδίο ορισμού
Α
( )
f A
Σύνολο τιμών
( )
f A
Α
Συσχέτιση:
( )
( )
f x y g y x
= Û =
Προκύπτει έτσι πως η g αποτελεί την αντίστροφη διαδικασία της
f και για αυτό
την ονομάζουμε
αντίστροφη συνάρτηση
της
f
και τη συμβολίζουμε με
1
f
-
.
Επομένως:
( )
( )
1
f x y f y x
-
= Û =
Άρα:
( )
(
)
1
f f x x, x A
-
= Î
και
( )
(
)
( )
1
f f y y, y f A
-
= Î
10. Ορισμός
Όρια και Πράξεις
Αν υπάρχουν τα όρια των συναρτήσεων f και g στο
0
x
, τότε υπάρχουν τα πα-
ρακάτω όρια και ισχύει
:
1.
( ) ( )
(
)
( )
( )
0
0
0
x x
x x
x x
lim f x g x lim f x lim g x
®
®
®
+ =
+
f
A
f(A)
g(y)=x
y=f(x)
g









